Charged particles in motion exert a magnetic force on each other. We will introduce some of the mathematical machinery to make analyzing magnetism possible.
Key Terms
o Vector product
o Cross product
o Right-hand screw rule
o Magnetic force
o Field
o Unit charge
o Electric field
o Magnetic field
Objectives
o Define the vector product of two vectors
o Define the concept of a field
o Recognize the magnetic field, force, and their relationship
o Calculate the force on a moving charged particle in a given magnetic field
Let's Begin!
We know that static (stationary) electric charges produce forces on one another. But what if these charges are moving? As it turns out, moving charge produces another force that acts on other charges: the magnetic force (or magnetism). In this article, we will introduce the magnetic force as well as the magnetic field. To understand magnetism, we must first consider another aspect of vectors: the vector product (or cross product).
The Vector Product
We know that we can multiply two vectors in such a way that their product is a scalar; in this way, we defined the scalar product (or dot product) of two vectors. We can, in a similar manner, define a multiplication operation that produces a resulting vector: we call this operation the vector product (or cross product ) of two vectors. The vector product multiplies two vectors such that the resulting vector is perpendicular to both of the other two vectors. Thus, the vector product is only defined in three dimensions.
A three-dimensional vector is similar to a two-dimensional vector; we simply add a third spatial coordinate (or direction), which we typically denote as z. Thus, we might represent a three-dimensional vector as (x, y, z) or as xx + yy + zz. Drawing a diagram in two dimensions (such as on a piece of paper or a computer screen) can be somewhat challenging, but it can be done fairly convincingly. For instance, the vector (2, 3, 3) is drawn in the diagram below using something of a perspective technique for the axes.
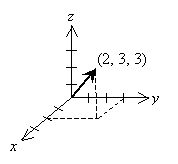
Given two vectors A = (a1, a2, a3) = a1x + a2y + a3z and B = (b1, b2, b3) = b1x + b2y + b3z , the vector product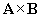 
is defined as follows.
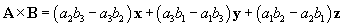
This formula is, of course, a little convoluted and admittedly difficult to memorize. (Advanced students with some knowledge of linear algebra can note that this result is simply the determinant of the matrix below.)
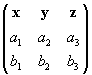
Note that the vector product is not commutative; that is to say,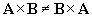 
. One can easily show, however, that 
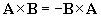. As mentioned above, the vector product of two vectors yields a third vector perpendicular to those vectors. Let's take a simple case: let A = x and let B = y. Two vectors are perpendicular to both x and y: z and –z. Let's see what result the vector product produces (note that in the formula above, only a1 and b2 are non-zero):
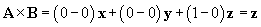
Let's take a look at a diagram of the results.
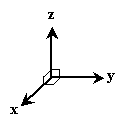
Note that the positive z vector is the result. (Also note that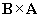 
is –z. ) But we can also use the so-called right-hand screw rule to determine which of the two possible vectors is correct. Let's look at the above diagram from a different angle: z will be down into the surface of this page.
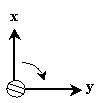
If we placed the tip of a right-hand screw (as shown in the diagram) at the vertex of x and y, we would turn it in the clockwise ("right-hand") direction to drive it into the surface of the page. Thus, we can find the correct vector result of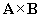 
by determining which direction a screw would go when turned from A to B (by way of the smaller of the two possible angles).
In some cases, the unwieldy expression for the vector product need not be used. As we discussed above, we can determine the direction of the vector product by using the right-hand screw rule. We can determine the magnitude of the vector product using the following simple relation, where A is the magnitude of A, B is the magnitude of B, and ? is the angle between the two vectors. (Recall that the straight brackets | | simply mean "magnitude.")
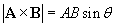
The following practice problems provide an opportunity to apply these concepts to some specific mathematical situations.
Practice Problem : If A = 3x and B = –2z, what is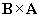 
?
Solution: We have two possible approaches to this problem. Let's try both and show that they are equivalent. First, we'll use the formula for the cross product.
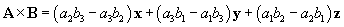
Now, 
, meaning we can still use the above expression as follows.
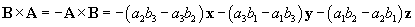
According to our notation, a1 = 3 and b3 = –2; all other terms are equal to zero.
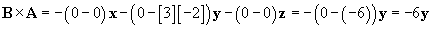
Let's now try our other approach. First, we'll calculate the magnitude of the vector product. Note that x and z are perpendicular: the angle between them is thus 90°.
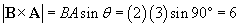
This result agrees with our previous result so far. Now, we will use the right-hand screw rule to find the direction of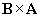 
.
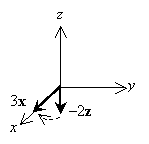
Notice that if we turn a right-hand screw in the direction shown (from B to A ), we see that a right-hand screw would drive in the negative y direction. Thus, combining this result with the magnitude we calculated above, we again find that the vector product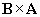 
is –6y.
Practice Problem :
Calculate the vector product of 3x – y + z with 2y – 4z (in that order).
Solution: In this case, using the formula for the vector product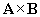 
is the simplest approach. We note in this case that a1 = 3, a2 = -1, a3 = 1, b1 = 0, b2 = 2, and b3 = -4.
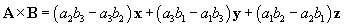
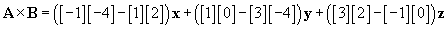
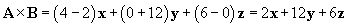
The result is therefore 2x + 12y + 6z.
Magnetism
As it turns out, moving charges exert other forces other than the simple Coloumb (electrostatic) force. The force on one moving charge resulting from another moving charge is called the magnetic force. A full understanding of magnetism requires calculus, so we will limit the breadth of our discussion of the subject somewhat. An important concept in the discussion, however, is the concept of a field, which is a vector quantity that defines the force on a unit charge (a 1-coulomb particle). For instance, the electric field is the electric force that a 1-coulomb particle would experience at a particular location. Recall that we define the electric force (in newtons) as follows:
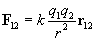
Let's say we have a charge q, and we want to calculate the electric field E produced by this charge. Remember, the electric field is the force per unit charge--thus, we can simply divide out the second charge from the force F 12 to get the electric field.
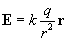
This expression is the electric force that would be applied to a unit charge located a distance r (in the r direction) from the location of the existing charge q. (The electric field is measured in units of newtons per coulomb.) If we want to find the force on a particle of charge qa, we simply need to calculate the product qaE. We can depict the field by drawing arrows that indicate the direction of the force (and field) at various locations in the space around the charge q. This type of drawing is not entirely accurate, but it is a helpful tool in representing a field visually. The charge q is shown as a central dot, and the "field lines" are shown as bold arrows.
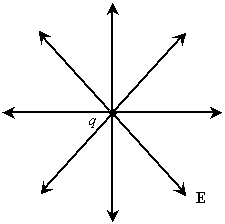
The field diagram shows that a unit charge (which is positive) placed somewhere around the charge q (which is also assumed to be positive) would experience a repulsive ("pushing") force away from q. Hence, all the field lines are directed away from q.
A similar field concept can be applied to magnetism. We want to describe the magnetic force mathematically, and this endeavor is aided by the definition of the magnetic field. (The magnetic field has a slightly more complicated definition than the electric field: its magnitude is proportional to the force that would be applied to a unit charge--1 coulomb--moving at a unit velocity--1 meter per second.) The magnetic field (sometimes called the magnetic flux density) is often represented using the symbol B and has units of teslas (T). (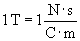
.)
Although we will not calculate B for specific situations because the math is beyond the scope of this article, we can consider an example situation where a magnetic field is produced. For instance, a current-carrying wire produces a magnetic field, as shown below. We represent the current in the wire as a vector i. Also, we show the wire from two perspectives: a "sideways" perspective (top) and an "on-end" perspective (bottom). In the latter case, the current is going into the surface of the page. Here, we use a field diagram approach similar to that of the electric field shown above. The field lines (arrows) simply show the direction of the force at some representative positions in space.
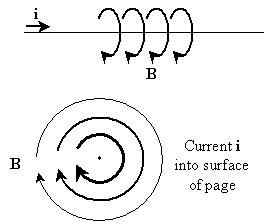
Note that the magnetic field "circulates" around the wire, unlike the electric field, which "diverges" from the central charge. As it turns out, the magnitude of the magnetic field diminishes with increasing distance from the wire (this is a sensible result--the farther one is from the wire, the less influence it has). You can even show through a simple experiment that a current-carrying wire produces a magnetic field (force): simply connect a wire to both ends of a battery (not for too long though--this quickly drains the battery!) and bring a navigational compass near the wire. You will see the needle of the compass deflect in response to the magnetic field that you have produced. Disconnect the wire, and the compass needle will return to its original orientation.
We can now introduce an expression for the magnetic force on a charged particle moving through a magnetic field. Assume that the particle has a charge q and that it is moving with velocity v in a magnetic field B. The magnetic force F B is the following.
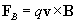
Note that we must employ the vector product in this case; thus, the direction of the force is not simply the direction of the magnetic field (B ), nor is it simply the direction of the particle's velocity (v ). We can calculate the magnitude of this force using the properties of the vector product that we discussed previously, where ? is the angle between the vectors v and B.
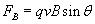
To be sure, these formulas can be difficult to understand by themselves. The precise relationship between the math and what the math is attempting to describe may not be entirely clear to you. The following practice problem, however, illustrates the use of these expressions. Through practice and use, you can improve your understanding of the meaning of the math.
Practice Problem : A particle with a charge of 10-3 coulombs is moving in the x direction with a speed of 30 meters per second. If it is passing through a magnetic field of magnitude 2 teslas pointing in the z direction, what is the magnetic force on the particle?
Solution: Let's write out each of the necessary parameters for calculating the magnetic force on the particle. First, the charge q of the particle is 10-3 coulombs. Second, the velocity v of the particle is 30x meters per second. Third, the magnetic field B through which the particle is traveling is 2z teslas. So we use the following formula:
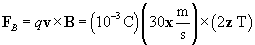
Notice that we are crossing a vector in the x direction with a vector in the z direction; thus, following the right-hand screw rule, the result should be a vector in the negative y direction. Furthermore, because the x and z vectors are perpendicular, the magnitude of the result should simply be the following.
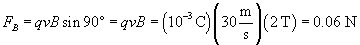
Thus, F B = –0.06y newtons. You can also calculate the same result using the more complicated formula for the vector product.
