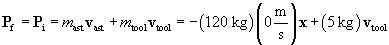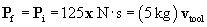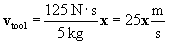How to Calculate Momentum

We will define the concept of momentum in the context of physics and use the mathematics of vectors and differences (such as the difference in time, ?t) to derive the law of conservation of linear momentum and to apply it to various problems.

Key Terms

o         Momentum

o         Law of conservation of linear momentum

Objectives

o         Understand the physical definition of momentum

o         Derive the law of conservation of linear momentum

o         Apply this conservation law to solving problems involving linear motion

Let's Begin!

We have used the concepts of mass and velocity to describe the motion of objects. Imagine two objects, one with a small mass and one with a large mass; consider, for instance, a tennis ball (less massive) and a medicine ball (more massive). Now, imagine the two objects being thrown at you at some speed v; obviously, getting hit by a tennis ball traveling at speed v sounds much less painful than getting hit by a medicine ball traveling at speed v. Consider also the medicine ball traveling at two different speeds: a slower speed, s, and a faster speed, f. Trying to catch a medicine ball traveling at speed s (the slower speed) certainly sounds easier than trying to catch one traveling at a faster speed f! We tend to think of a larger object traveling at a particular speed as having more momentum than a smaller object traveling at that speed. Likewise, we think of one object traveling at a fast speed as having more momentum than that object traveling at a lower speed. Momentum, therefore, increases with increasing speed as well as increasing mass. This situation fits logically, then, with the definition of momentum in physics. The momentum p of an object of mass m and velocity v is defined according to the following relationship:

p = mv

Notice that momentum, like velocity, is a vector with both magnitude and direction. As the mass or velocity of an object increase, so does the momentum.

The Relationship Between Momentum and Force

Recall that acceleration is simply the time rate of change of velocity. Thus (on average), we can write the following:

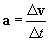
Let's substitute this into our force expression from Newton's second law of motion:

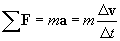
Assuming the mass m remains constant, we can make the following change:

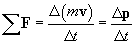
Note that because mv appears in the net force expression, we can write it in terms of momentum p. The net force on an object is therefore the time rate of change of its momentum.

Practice Problem: A 50-kilogram object is moving at a speed of 10 meters per second. What is its momentum?

Solution: The momentum, p, of the object is simply the product of its mass and its velocity: p = mv. Because no direction is specified, we are only interested in determining the magnitude of p, or p. Thus,

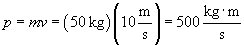
Note the units in the result--we can also express the units in terms of newton seconds.

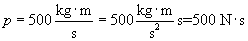
Let's now consider some arbitrary number of objects; the total momentum P of the system of objects is simply the sum of all the individual momenta: 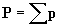. In the same manner, following Newton's second law, we'll call F_tot the sum of all the forces acting on the objects. But this sum, F_tot, is simply the sum of all external forces acting on the system of objects. Then,

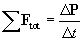
And if no external forces are acting on the system of objects,

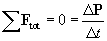
In other words, the time rate of change of the total momentum of the system of objects is zero in this case; this is simply a statement of the law of conservation of linear momentum for a closed and isolated system. That is to say, the total momentum is constant for a given system of objects on which no external force acts. This conclusion is extremely useful for problems involving, for instance, collisions of objects. The following practice problems allow you to explore the implications of this result.

Practice Problem: A projectile of mass 1 kilogram traveling at 80 meters per second collides head on with another projectile of mass 2 kilograms traveling at 60 meters per second in the opposite direction. If the projectiles "stick" together after their collision, what is their velocity after colliding?

Solution: Let's draw a diagram of the situation before and after the collision. We also define the direction x for reference.

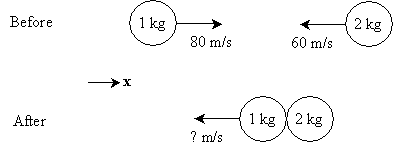
From the lesson we learned that the total linear momentum of a system of objects must be conserved (that is, unchanged) if no external forces act on that system. In this case, it is assumed that no forces outside the system act upon the two objects. The total momentum before the collision must therefore be the same as the total momentum after the collision. Let's first calculate the total momentum before the collision (P_i):

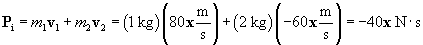
After the collision, because the two objects "stick" together, they effectively become a single object with a mass of 3 kg and some velocity v. The momentum of this object, P_f, is

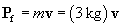
We want to calculate v, which is the velocity of the objects after collision. Because the momentum before the collision is the same as that after,

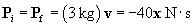
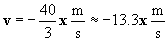
Thus, the velocity of the objects after collision is 13.3 meters per second in the same direction as that of the larger object before the collision (which we have defined here as the negative x direction).

Practice Problem: An astronaut with all his equipment and tools has a mass of 125 kilograms. An accident occurs in space, causing him to become detached from a space station and to drift into space at a speed of one meter per second. One of his tools weighs five kilograms, and decides to use it to get back to the station. If he throws the tool directly away from the station, what is the minimum speed at which he must throw it to get himself moving back toward the station?

Solution: As usual, we can greatly assist the problem-solving process by drawing a diagram of the situation. The diagram need not be artistic--simple figures are often sufficient for representing different objects.

Part of the astronaut's weight is a five-kilogram tool; if he throws this away from himself (and also directly away from the station) with sufficient velocity, he can (by conservation of momentum) cause himself to begin moving back toward the station. This situation is illustrated below. Note that the mass of the astronaut decreases by five kilograms when he throws the tool away.

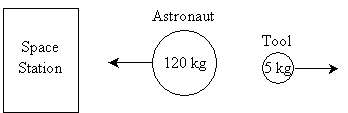
We can use the law of conservation of momentum to calculate the speed at which the astronaut must throw the tool to reverse his alarming course and send him back toward the station. The initial total momentum of the astronaut, P_i, is the following. We'll define as x the direction away from the station.

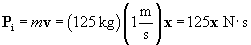
This must also be the total momentum of the astronaut and the tool after he throws it away--we'll call this final momentum P_f. Let's calculate the speed of the tool required to bring the astronaut to a stop; any speed above this number will cause the astronaut to move toward the station.