By taking a look at parallelism and perpendicularity in three dimensions, we see that many of the same principles apply but that several complexities are also added.

Key Terms

o Skew lines

o Axes

o Cross section

Objectives

o Recognize perpendicular, parallel, and skew lines in three dimensions

o Be able to represent simple three-dimensional figures using two-dimensional drawings

o Know what a cross section is and how it can be used to relate two- and three-dimensional geometry

Objects in real-life have three spatial dimensions, so it is helpful for us to understand some of the fundamental aspects of three-dimensional geometry. In many ways, three-dimensional geometry is just an extension of two-dimensional geometry; many of the same principles apply. In this article, we consider parallelism and perpendicularity in three dimensions, and we then take a look at drawing three-dimensional figures on a two-dimensional surface. Finally, we look briefly at cross sections.

Parallelism and Perpendicularity in Three Dimensions

In two dimensions, we noted that any two lines that do not intersect are parallel. Recall, however, that we gave a slightly more fundamental definition that involved the relationship of the angles formed by a transversal that cuts across the parallel lines. Now, imagine two lines in three dimensions. In three dimensions, you can probably easily imagine two lines that are not really parallel but that do not intersect, either. An example is shown below using lines l and m, where one of the lines (l) is shown "on end" (that is, going into and out of the surface of the page) so that it appears as a point.

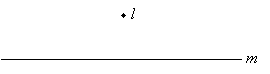
Notice that the two lines do not have any point of intersection, and yet, they are not what we would consider "parallel." These are what we call skew lines. Note also that these lines, although they look in some sense like they are "perpendicular," are not truly so because they do not intersect. If they did intersect, however, then they would indeed be perpendicular, as shown below.

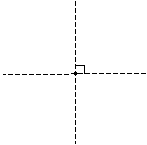
In two-dimensional (planar) geometry, for a given point on a line, there exists only one perpendicular line, as shown below.

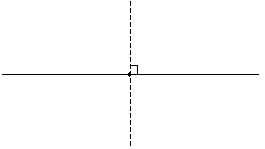
In three-dimensional geometry, there exist an infinite number of lines perpendicular to a given line. Consider a line l that intersects a plane at a right angle (in other words, wherever an angle measurement is taken around the line with respect to the plane, it is always 90°). We can draw innumerable lines in the plane that intersect line l; because they lie in the plane, they intersect l at a right angle.

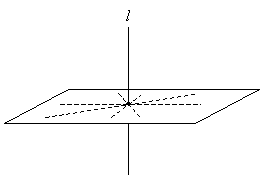
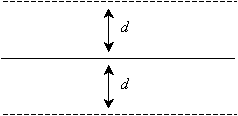
Likewise, in planar geometry, there exist only two lines that are parallel to a given line for some fixed distance d, as shown below.

In three-dimensional geometry, once again, there exist an infinite number of lines parallel to a given line for some fixed distance d. Imagine the line l passing at a right angle through a plane once again, as shown above. This time, however, let's draw a circle with radius d in the plane.

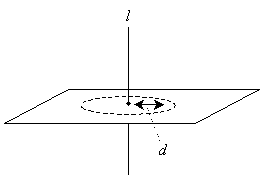
Now, we can draw any number of lines that intersect the circle and the plane at a right angle-these lines are also parallel to l.

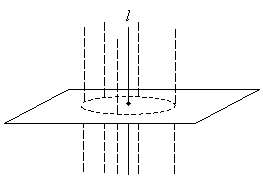
We can define parallelism and perpendicularity for planes in three dimensions similarly to the way we defined them for lines in two dimensions. Any two intersecting planes (that are not the same plane) form a line of intersection; this is the three-dimensional analog of a point of intersection for two lines. Such an intersection of two planes is shown below.

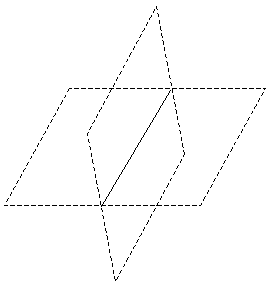
If two planes do not intersect, then they are parallel. If the angle of intersection is 90°, then the planes are perpendicular. This angle of intersection is measured by looking at the planes "on edge," such that the line of intersection is perpendicular to the surface of this page, as shown below. (Notice that when looking at the planes from this perspective, they appear to be lines, and the line of intersection appears to be a point.)

 

Thus, we can see that parallelism and perpendicularity in three dimensions, although they bear resemblance to the same concepts in two dimensions, take on a slightly more complicated character. Nevertheless, by extending what we have already learned in two dimensions, we can understand geometric concepts in three dimensions as well.

One might wonder if geometry can be extended to four or more dimensions. The answer is yes, but such an endeavor becomes much more difficult because we do not have any experience in reality that helps us conceive of a geometric space with more than three dimensions. For instance, although we readily understand the concepts of up-down, left-right, and forward-backward (the three spatial dimensions), we have a very difficult time conceiving a fourth dimension. What would such a dimension (or direction) look like? Such multidimensional geometries do play an important role in certain fields of study, but they are not nearly as applicable to everyday life as two- and three-dimensional geometry.

Practice Problem: Show that two lines that are cut by a transversal, thereby forming congruent corresponding angles, are not necessarily parallel in three-dimensional geometry.

Solution: This problem requires us to apply some critical thinking regarding lines and planes in three dimensions. First, let's start with two lines that we will assume are parallel, and let's cut these lines by a perpendicular transversal, as shown below.

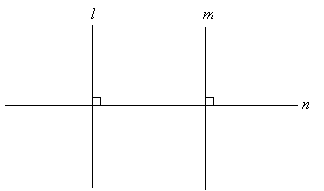
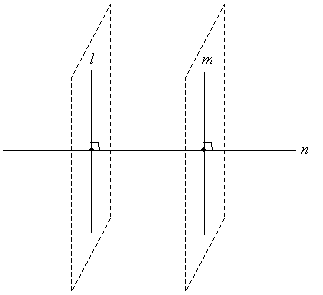
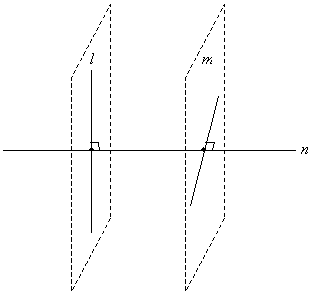
Thus, even though corresponding angles for lines l and m cut by transversal n are congruent (they are all 90°), the lines are not necessarily parallel.

Drawing in Three Dimensions

Obviously, it is difficult to draw a figure in three dimensions when one is using a two-dimensional sheet of paper (or computer screen). Nevertheless, we can very easily make drawings that look three-dimensional by following a few simple rules. First, define directions (rays) for each dimension. Although it is not necessary, it is sometimes helpful to draw a set of axes, such as those shown below.

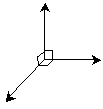
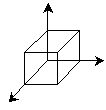
Note that we have shown that the axes are all mutually perpendicular-just as the directions left-right, up-down, and backward-forward are all perpendicular. To draw a figure that has a three-dimensional appearance, use distances parallel to a particular axis to create the illusion that a figure is extended in that direction. Note, for instance, how a cube shows three-dimensional character by virtue of its relationship with the axes (even if you ignore the axes, the same effect is achieved).

Practice Problem: Use a set of axes to draw a triangle that appears to be "leaning over" in three dimensions. (In other words, the plane formed by the triangle is not parallel with the surface of this page.)

Solution: Start by drawing a set of axes, as we did in earlier.

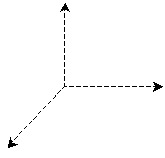
Now, let's pick three points for the triangle, and let's place one at some point on each axis. This will create the effect of the triangle having extent in three different directions (dimensions). Finally, connect the points, as shown below.

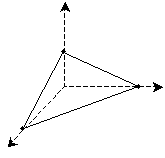
Thus, we have created a triangle that appears to be "leaning over" in three dimensions. To be sure, the triangle is still just a two-dimensional drawing, but by using the axes, we can create the illusion (albeit in a somewhat simplistic manner) that the triangle is "slanted" relative to the surface of the page.

Cross Sections

Consider some three dimensional figure, such as a cylinder; next, imagine a plane that cuts through that figure, as shown in the example below. The intersection of the plane and the three-dimensional figure is called a cross section, and it is a two-dimensional "slice" (of infinitesimally small width) of the figure.

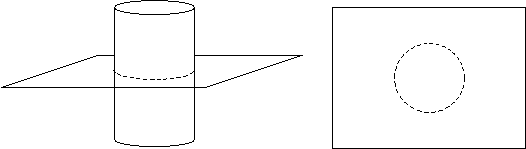
In the example above, the plane of the cross section is perpendicular to the vertical orientation of the cylinder-the cross section is thus a circle. If use a different angle, however, we end up with an oval instead of a circle for the cross section.

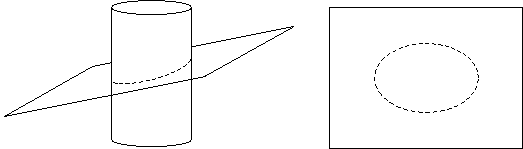
Thus, we can see that two-dimensional geometry can in some sense be seen as a "cross section" of three-dimensional geometry.

Practice Problem: What two-dimensional figures are formed by taking the cross section of a sphere (a racquetball, for instance, is an example of a sphere)?

Solution: Recall that a cross section is simply a planar "cut" of the figure. Thus, let's draw a plane and a sphere.

Now, a cross section is formed by lowering the sphere (in this case) into the plane, just as we might lower it into a pool of water. Because the sphere is perfectly symmetric, the resulting cross section is always a circle. Depending on where the cross section is taken relative to the center of the sphere, the circle may have a radius ranging from zero (the plane is tangent to the sphere, or just touches it at a point on the surface of the sphere) to the radius of the sphere.