Key Terms
o Force
o Velocity
o Acceleration
o Newton's first law of motion (law of inertia)
o Net force
Objectives
o Know how to add and subtract vectors
o Recognize the relationship between a net force and the sum of vectors
o Apply vectors and their sums to understanding Newton's first law of motion
Let's Begin!
A fundamental concept in physics is the idea of a force. Although we may have a difficult time attempting to define this term, we have a pretty good idea of what is meant when someone talks of "applying a force" to some object. We can see forces at work when an object falls under the influence of gravity, or when two billiard balls collide, causing changes in their motion. A force, then, is an influence on the motion (or lack thereof) of an object. We can think of forces as being stronger or weaker (that is, they have a magnitude), and we can think of forces as being directed one way or another (that is, they have direction). Thus, a force is a prime candidate for representation as a vector. We will consider forces in terms of Newton's laws of motion, and in doing so, we will further discuss the properties of vectors and how they can be used to study the motion of objects.
Force, Vectors, and Newton's First Law of Motion
Another important quantity that we will represent using vectors is velocity, which is the speed of an object in a particular direction. Likewise, acceleration can be represented using vectors. Acceleration is simply the rate of change of the velocity; acceleration also has a magnitude and a direction. The direction of the acceleration can be parallel to the velocity (which increases the speed of the object in its "forward" direction), antiparallel (opposite in direction) to the velocity (which decreases the speed of the object in its "forward" direction), or it can be at an angle oblique to the velocity (which causes the object to change its "forward" direction).
Newton's first law of motion (sometimes called the law of inertia ) states that if no net force acts on an object, then that object will not experience a change in its motion (that is, an acceleration). A common way of stating this principle is that an object at rest tends to stay at rest, and an object in motion tends to stay in motion, unless acted upon by a net force. What is a net force? A net force is the sum of all the forces acting on an object. For instance, gravity tends to pull an object down towards the Earth, but if that object is supported by a table, for instance, then it doesn't fall. In this latter case, the table exerts an upward force on the object that exactly matches gravity--the object therefore remains at rest, because the net force is zero. If the table is removed, however, the net force is downward because of gravity--the object then falls. These two situations are illustrated below.
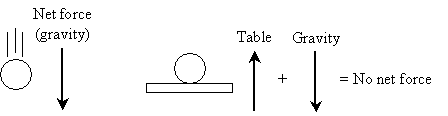
The above case is simple; the forces are equal in magnitude and opposite in direction, so it is fairly obvious that they cancel. What happens in cases where multiple forces have different magnitudes and directions? To handle this case, we must determine how to add (and subtract) vectors.
Note from our example above that two vectors equal in magnitude and opposite in direction sum to zero. Since vectors have no location, what if we simply attach the tail of one vector to the head of another? Let's use the following graphical approach; we'll simply translate one of the vectors such that its tail is at the same point as the head of the other vector, as shown below.
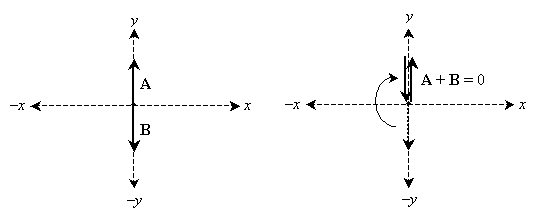
Note that if we follow the vectors like a path, we start at the origin and end at the origin. Thus, the tail and head of the resulting vector are both at the origin, meaning that it is a vector of magnitude zero. Let's try this with a slightly more complicated (but similar) set of vectors. Imagine the origin as some object, and the vectors each represent a force on the object. We add all the vectors using our "head-to-tail" method to find the net force.
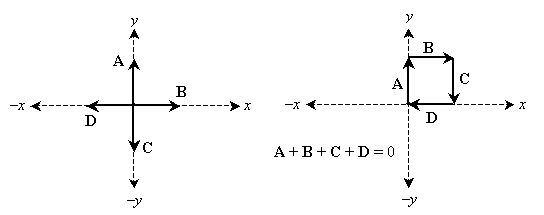
Again, we start at the origin and end at the origin, meaning that the net force vector is zero. But this makes perfect sense: the vertical forces are equal in magnitude but opposite in direction, as are the horizontal forces. Imagine four men each pushing on the object with the forces illustrated above--their efforts cancel each other, and the object remains at rest. What about forces that do not cancel? Let's consider another example.
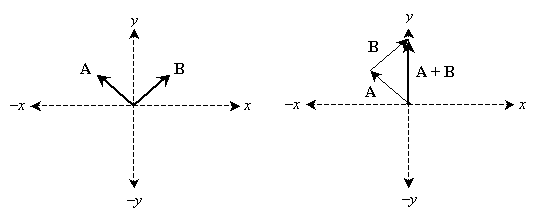
Both forces in the example above have an "upward" direction, but their horizontal leanings are opposed. In this case, the net force is then directed upwards. In this case, an object that experiences the net force shown above would not fall under the conditions of Newton's first law; the motion would experience acceleration in the upward direction. Note that it doesn't matter what order we add the vectors as long as we use the "head-to-tail" approach; in other words, vector addition is commutative. (Vector addition is also associative.) Vector addition (and subtraction) can be performed mathematically, instead of graphically, by simply adding (subtracting) the coordinates of the vectors, as we will see in the following practice problem.
Practice Problem : Consider vectors A = (3, 2) and B = (–1, 3). What is the sum A + B ? What is A – B ?
Solution: One approach is to plot these vectors on a set of axes and solve the problem graphically. From this approach, we can also see how we can solve the problem without having to use a graph.
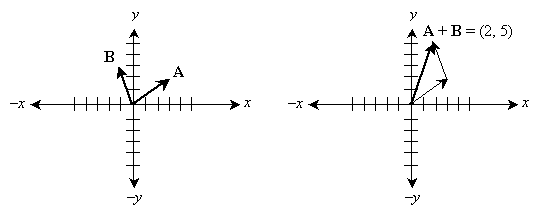
So, how can we solve this problem without having to manipulate the graphs of the vectors? Note that the head of vector A becomes the tail of vector B ; thus, we need only translate B by the head coordinates of A . In other words, simply add the coordinates of A and B !
A + B = (3, 2) + (–1, 3) = (2, 5)
The same approach can be used for any arbitrary number of vectors. What about subtraction? Subtraction is analogous.
A - B = (3, 2) – (–1, 3) = (4, –1)
Subtraction is simply addition of a negative value (A – B = A + (–B )). Graphically, a negative vector is simply the vector with its head and tail reversed, as shown below.

Practice Problem : An object has three forces acting on it; these forces can be represented by vectors A = (3, 2), B = (–1, 3), and C = (–2, –5). Determine if the object is experiencing any acceleration.
Solution: We can calculate the net force by adding the vectors A, B, and C.
A + B + C = (3, 2) + (–1, 3) + (–2, –5) = (3 – 1 – 2, 2 + 3 – 5) = (0, 0)
Thus, the object is experiencing no net force. By Newton's first law of motion, the object is therefore experiencing no acceleration: if it is at rest, it remains at rest, and if it is moving with some velocity, then its velocity will remain constant. If you are not sure about the math above, try graphing these vectors to prove the result visually.
Components of Vectors
Because we can add vectors in this manner, we can also easily see that every vector can be represented as the sum of a vector in the x (or negative x) direction and a vector in the y (or negative y) direction. An example is shown below for vector V .
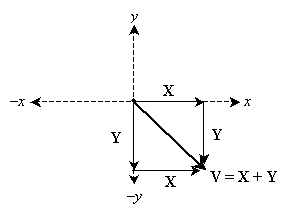
In some cases, it is helpful to be able to divide a vector into its component parts in the x and y directions. Vectors X and Y can each be represented as a magnitude multiplied by a unit vector. The respective unit vectors are (1, 0) for X and (0, 1) for Y (note that both of these unit vectors have a magnitude of unity). We'll denote these unit vectors with lower-case notation: x and y. Now, we need only determine the magnitudes of X and Y. But this is simple; let's write out the vector addition.
V = X + Y = |X | (1, 0) + |Y | (0, 1) = (|X |, |Y |)
The magnitude of X is simply the x-coordinate of the vector V , and the magnitude of Y the y-coordinate of V. In other words, if V = (4, 9), for instance, then
X = (4, 0) = 4?(1, 0) = 4x
Y = (0, 9) = 9?(0, 1) = 9y
Also note in the above graph that the vectors form a right triangle; thus, we can use right triangle trigonometry to find the "lengths" (magnitudes) of X and Y.
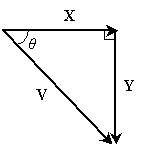
From the Pythagorean theorem, we know the following (recall the use of the absolute value notation for the magnitude--or length--of a vector):

Furthermore, from right triangle trigonometry we know that
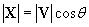

Thus, we can write the vectors X and Y as follows.
X = x |V | cos ?
Y = y |V | sin ?
Practice Problem : Find the components of the vector (3, –7) in the x and y directions.
Solution: We can write the vector (3, –7) as the sum of two vectors, one in the x direction and one in the y direction. The corresponding unit vectors are x = (1, 0) and y = (0, 1); obviously, then the components are (3, 0) for the x direction and (0, –7) for the y direction.
Practice Problem : A force vector has a magnitude of 5 units and forms an angle of 30° above horizontal. What is the component of the force in the vertical direction?
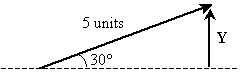
Now, we want to find the component (magnitude) of the given vector in the horizontal direction; this result is labeled Y in the drawing above. Thus, we want to find the magnitude of Y. We can use right triangle trigonometry to do this.
|Y | = (5 units) sin 30° = (5 units) (0.5) = 2.5 units
Thus, the force has a component of 2.5 units in the vertical direction.