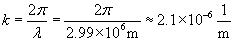o         Electromagnetic wave

o         Electromagnetic radiation

o         Ether

o         Permittivity of free space

o         Permeability of free space

Objectives

o         Show conceptually how accelerated charge produces electromagnetic waves

o         Determine the speed of light in a vacuum using material parameters

o         Describe an electromagnetic wave using a sine function

o         Calculate the frequency and wavelength of different electromagnetic waves

Let's Begin!

As it turns out, electromagnetic waves (light) obey many of the same mathematical relations of mechanical waves, although the physical aspects of electromagnetic waves differ in many ways from those of acoustic waves.

The Source of Electromagnetic Waves (Light)

The electric force arises from the presence of charge; the magnetic force arises from charge in motion. But what happens if we accelerate a charged particle or object? The result is an electromagnetic wave, or light (in common parlance, the term light usually refers to the visible portion of the electromagnetic spectrum--most electromagnetic waves, however, are invisible). Let's try to imagine what happens by considering the field around an electric charge. Assume that the charge is accelerated over some small distance from rest to a final velocity v_f. We know what the field looks like for a charged particle at rest; the field for the particle moving at speed v_f has the same shape (still centered on the charge, of course).

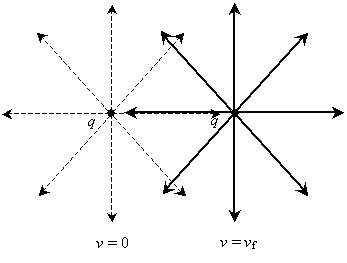
Assuming "information" about the particle's location travels at a finite speed (a very important assumption: essentially, it simply means that the change in the electric field between the initial and final positions does not take place instantaneously throughout space), some distortion of the field must take place. Below is a series of approximate renderings showing how the field is distorted by the acceleration of the charged particle. The particle is shown initially at rest (v = 0), then at a velocity v_f at two later times.

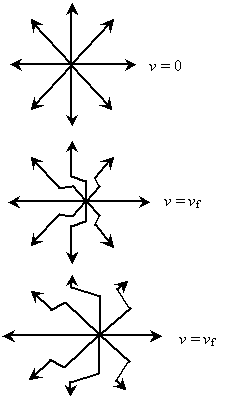
Notice that an acceleration of the charged particle (between the first and second field diagrams above) causes a distortion in the field, which then propagates outward (as shown between the second and third diagrams above). This propagating (traveling) distortion is an electromagnetic wave. (Because the charged particle is in motion, the magnetic field also shows this propagating wave behavior. The classical relationship between the electric and magnetic fields is described by Maxwell's equations--a topic that is beyond the scope of this article.)

The Speed of Light

Following up on our assumption that electromagnetic waves have a finite speed, we might endeavor to determine what that speed is. As with the speed of sound, the speed of light varies depending on the medium in which it travels, but unlike sound, light is able to travel in a vacuum (such as space). A vacuum, in some sense, is the complete absence of any material; the fact that electromagnetic waves (sometimes called electromagnetic radiation) can propagate (travel) in a vacuum gives rise to at least two trains of thought. One supposition is that the vacuum actually has some material permeating it (this supposed material is sometimes called ether). Another supposition is that electromagnetic waves do indeed propagate in the absence of a medium; this supposition eventually leads to the theory of special relativity (another topic beyond the scope of this article). Regardless of which answer to this problem is correct, we can still use material parameters (even in the case of a vacuum) to relate the speed of light to the medium, just as we did with sound.

Recall from our discussion of the electric force that we had to deal with a constant k defined as follows.

Note that the parameter ?₀ appears in the expression. This is the electric material parameter associated with a vacuum, and it is called the permittivity of free space. The value of ?₀ is about 8.85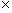10^-12 farads per meter. A similar constant appears in expressions for the magnetic field in a vacuum (a topic that we did not discuss in great depth): ?₀. This constant is called the permeability of free space and has a value of about 1.26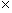10^-6 henrys per meter (one henry is equal to one tesla square meter per ampere: 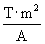). (These permittivity and permeability values are different in a material, such as rock or plastic, for instance.) In our discussion of acoustic waves, we found that the wave speed v obeyed the following expression, where B is the bulk modulus and ? the density of the material.

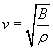
As it turns out, the speed c of electromagnetic waves (in a vacuum) is the following:

The speed of light is (an extremely fast) constant in a vacuum. Notice that the forms for the speed of light and of sound are (perhaps coincidentally) very similar. In fact, if we wrote the speed of sound v using the compressibility (which we might call C--the reciprocal of B), the forms are essentially identical.

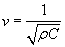
One important way in which electromagnetic waves differ from sound waves is that an electromagnetic wave is in fact a vector wave: it has both a magnitude and a direction (as we can see in the field diagrams above). Sound waves, by contrast, are scalar waves: they have only magnitude. An expression for the electric field portion of a traveling electromagnetic wave is given below. Note that the coefficient of the sine function is the electric field E, which is a vector quantity.

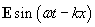
The factors ? and k are defined here in terms of the frequency f and wavelength ? just as they are in the case of sound waves. Furthermore, the speed of light c is related to the frequency and wavelength in the same manner.

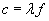
Practice Problem: Red light has a wavelength of about 650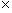10^-9 meters (650 nanometers). What is the frequency of this light?

Solution: We can use the relationship between c, ?, and f to calculate the frequency of red light. Earlier, we learned that the speed of light is about 2.99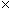10⁸ meters per second.

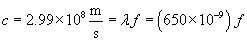
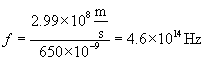
Thus, red light has a tremendous frequency of 4.6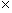10¹⁴ hertz--that is 460,000,000,000,000 oscillations of the electric and magnetic fields per second!

Practice Problem: A traveling electromagnetic wave has an electric field that obeys the expression 100y sin(628t - kx) volts per meter. What is the value k?

Solution: Recall that the factor k is equal to 2? divided by the wavelength, ?. We can also calculate the frequency f based on the value of ? = 630 hertz and use the speed of light, c, to calculate ?.

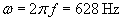
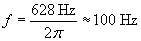
Now, use the relationship between ?, f, and c to find ?.

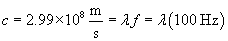
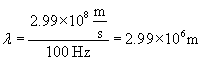
The wavelength is therefore almost 3 million meters. We can now calculate k.