Key Terms
o Angle
o Degree
o Straight angle
o Right angle
o Perpendicular
o Acute angle
o Obtuse angle
o Reflex angle
o Supplementary angle
o Vertical angle
o Parallel
o Transversal line
o Corresponding angle
Objectives
o Identify angles formed by intersecting lines and know how to use degree measurements in quantifying angles
o Use the relationships of angles formed by intersecting lines to calculate the measure of angles (when supplied with the proper assumptions)
o Know how parallelism is defined
o Recognize and use the relationships among angles formed when a transversal line cuts across two parallel lines
We begin taking an in-depth look at geometry by first considering parallelism and perpendicularity in a two-dimensional (planar) setting. As it turns out, how we define these concepts will determine the characteristics of the various figures that we will examine later. First, however, we consider the concept of an angle and how we can represent angles in geometric drawings.
Angles
An angle (or a set of angles) is formed whenever two lines (or some portions thereof) intersect. For instance, we might talk about how a hill rises from the level ground at a steep (or large) angle, or we might need to select an appropriate angle when constructing a roof on a house. Some common desktop tools for measuring or constructing angles are protractors and compasses. The diagram below shows two intersecting rays l and m that form an angle α, which is denotes using a small arc.
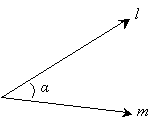

Obviously, the angle α can be larger or smaller depending on the orientation of l with respect to m. The diagrams below show an increasing angle α as you look from left to right.
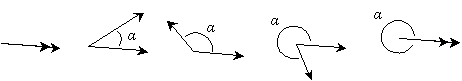

Notice that the angles start from zero on the left and increase to the point at which the rays have returned to their initial coincident positions. A common system of quantifying angles is degrees; the leftmost diagram above would be an angle of 0 degrees (or 0°), and the rightmost diagram above would be an angle of 360 degrees (or 360°). Below are some example angles with their associated degree measures.
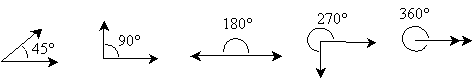

![]()
![]()
When two lines, line segments, rays, or some combination of any of these intersect to form a right angle, we say that they are perpendicular. We can also note that when two lines (or portions thereof) intersect, they actually form more than one angle.
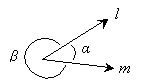

To differentiate these angles, we call an angle less than 90° an acute angle, and an angle between 90° and 180° an obtuse angle. Angles greater than 180° are called reflex angles. Angle α in the diagram above is less than 90°, so it is an acute angle; angle β is greater than 180° and is therefore a reflex angle. Note that the ray l forms an acute angle α with the ray m. If the ray l were to "rotate" all the way around until it sat on top of m, the angle α would then be 360°. As a result, we can note that the sum of the angles α and β must be 360° (l has "traveled" through an angle α, and it has an angle β to go before it reaches 360°--or equivalently 0°--where it started from). In other words, for the diagram above,
![]()
If two lines (or portions thereof) intersect as some place other than an end point, three or four angles can be formed. Note, however, that by the same reasoning that we used above, the sum of all the angles around the point of intersection is still 360°.
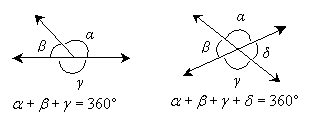

Note in the leftmost diagram that the endpoint of a ray lies on a line. Because the line can be thought of as two intersecting rays that point in opposite directions, the angle γ is 180°. Thus, the sum of α and β in this case is also 180°:
![]()
![]()
![]()
Because of this property, angles α and β are called supplementary angles. The same reasoning can be applied to the rightmost diagram above. In this case, however, two lines intersect, and we therefore have a number of relationships that we can immediately identify.
![]()
![]()
![]()
![]()
Let's apply a little algebra to these relationships. Consider, for example, the first and last expression above. We can equate these two expressions and manipulate them as follows:
![]()
![]()
We then arrive at the conclusion that angles β and δ are equal. In addition, we can use the same type of reasoning to conclude that angles α and γ are equal. Angles β and δ, as well as angles α and γ, are called vertical angles. Vertical angles are the pairs of opposite angles formed by the intersection of two lines.
Practice Problem: Given the intersecting lines n and m in the diagram shown below, find angle α.
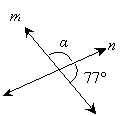
Solution: We know that supplementary angles sum to 180°. Thus, we can find angle α as follows.
![]()
![]()
Thus, α is 103°.
Practice Problem: Two line segments q and z intersect as shown below. Find angle t. Note: The greater angle between q and z is 121 degrees.
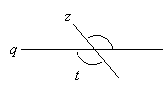
Solution: As we demonstrated earlier, vertical (opposite) angles formed by intersecting lines (or portions thereof) are equal. Thus, angle t is simply 121°.
Practice Problem: Identify the angles in the diagram below as acute, obtuse, or reflex, and find the unknown angle b.
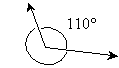
Solution: The angle of 110° is an obtuse angle (because it is between 90° and 180°). Angle b is a reflex angle and is equal to the difference between 360° and the obtuse angle, 110°.
b = 360° – 110° = 250°
Parallelism
Most people have a good sense of what is meant when someone says that two lines are parallel-for instance, if we were to ask what it means for two lines (in a plane) to be parallel, a simple answer might be that two lines are parallel if they do not intersect. We can, however, apply some mathematical rigor to this. Consider two lines l and m, which are shown below. Also, let's cut (intersect) these two lines by a transversal line, which is simply a line that intersects these two parallel lines. We'll call this transversal line n.
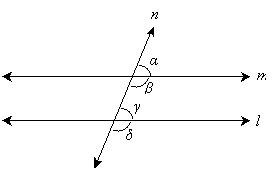
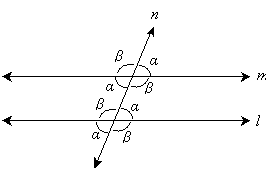
We can now state in a more mathematically precise manner what we mean when we say that two lines are parallel: two lines m and l are parallel if the angles β and γ sum to exactly 180°. As a consequence of this property, when lines m and l are parallel, angles β and δ are equal, as are angles α and γ. Imagine, for instance, that line n is the "flat ground," and lines m and l are towers; if we build these towers perpendicularly to n, then they go "straight up" and should never be expected to intersect.
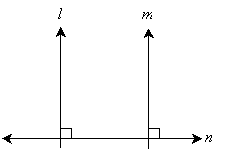
We can apply what we learned about vertical angles along with what we have discovered here to show that the first diagram with parallel lines has at most two unique angles. The angles α and the angles β, in this case, are called corresponding angles (that is, all the angles equal to α are corresponding angles, and all the angles equal to β are corresponding angles). Note, however, that these characteristics only apply when m and l are parallel, as we have defined this term above.
Practice Problem: Lines s and t are parallel, and they are cut by transversal line r. Find angle p.
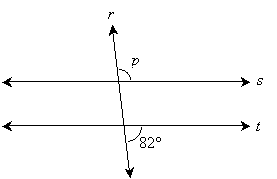
Solution: Because lines s and t are parallel, we can conclude that p must be 98° by the following reasoning. First, we know that by the rule of supplementary angles that the angles adjacent to the 82° angle must both be 98°.
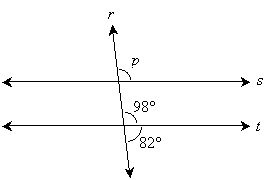
But this angle is a corresponding angle with p, and it is therefore the same. So, we conclude that p = 98°.

























