Key Terms
o System of linear equations
o Linear algebra
Objectives
o Recognize equations in multiple dimensions (beyond just two)
o Draw graphs of expressions that represent planes
o Solve systems of linear equations in multiple dimensions
Systems of Linear Equations
We can find the intersection of two lines by setting equal the functions that describe the lines. By solving this expression, we can obtain the solution (intersection). Likewise, we can also solve for the intersection (if it exists) of many linear functions in multiple dimensions by analyzing the associated system of linear equations. A system of linear equations is a set of equations (in some number of variables that may be greater than one or two) that must all be solved simultaneously. The area of mathematics that deals specifically with this type of problem is called linear algebra, which is a subject to which we could devote a course or two of its own! Because of its complexity, we will not deal with many of the aspects of linear algebra, but we will briefly cover what constitutes a system of linear equations and one reliable method for solving them.
A system of linear equations can be expressed in terms of multiple variables. So far, we have only dealt with two-dimensional equations: those that have an independent variable (one dimension) and that have a dependent variable (another dimension). We can plot such functions using a planar graph; if a third dimension is added, we can still use aspect drawings to create the illusion of a three-dimensional graph. Additional dimensions, however, become extremely difficult to visualize (spatially, our experience of the world is in three dimensions only). For the purposes of this section, we will only use variables x, y, and z to represent the three dimensions. The conventional arrangement of axes for a graph of a function in three dimensions is shown below.
In lesson 4, we solved some problems that involved two functions by equating the expressions. Let's briefly look at an example again, but let's write it using our x-y-z notation. This is actually a simple example of a system of linear equations.
y = 2x - 1
y = -4x + 3
Because these functions are expressed in a relatively simple form (the variable y is isolated on one side of the equation in both cases), the method of solution is also simple. The following, however, is an equivalent expression of the same system of equations.
2x – y = 1
4x + y = 3
Solving the system of equations expressed in this manner is essentially the same, but we give it a slight twist. We can solve just one of the equations for one variable or the other (usually whichever is easiest) and then use substitution to eliminate one variable from the other equation. This leaves an equation in one variable that can then be solved to find part of the solution. Let's use the example above to illustrate. We'll solve the first equation for y:
y = 2x – 1
Now, we substitute this expression into the second equation:
4x + y = 3
4x + (2x – 1) = 3
4x + 2x – 1 + 1 = 3 + 1
6x = 4
x = 
Finally, we substitute this value back into either expression to find the solution to the system of equations:
y = 2
– 1 = 
– 1 = 
The solution is then 
. We can check this result by substituting these values back into the original equations.
Let's now take a look at a system of equations in three variables. Although an additional variable (z) is added, the concepts and method of solution are all the same. Each equation can be graphed using an aspect drawing as a plane.
4x + y – 3z = 1
x – y + z = 4
–x + 2y – z = 3
Let's look at the graph of the second equation. One of the simplest ways to plot the graph of a plane is to calculate the intercepts for each axis-the intercept for the x-axis, for instance, is the value of x when y and z are both 0 (and so on for the other two variables). This leads to the intercepts in (x, y, z) notation of (4, 0, 0), (0, –4, 0), and (0, 0 ,4). Only a triangular portion of the plane is shown.
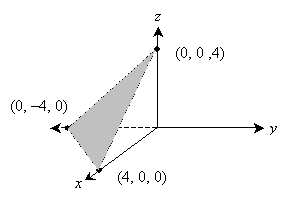
To solve, we once again choose an equation, solve for a variable, then substitute to eliminate that variable from the resulting expression. We must perform this process three times to reduce the system of equations to an equation in one variable. It is important that you not substitute from the same equation twice during this process: you will generally be unable to solve the problem. First, let's solve the first equation for y.
4x + y – 3z = 1
y = 1 – 4x + 3z
Substitute this result into the third equation and simplify.
–x + 2y – z = 3
–x + 2(1 – 4x + 3z) – z = 3
–x + 2 – 8x + 6z – z = 3
–9x + 5z + 2 = 3
–9x + 5z = 1
Now, let's substitute the result from the first equation into the second equation and likewise simplify.
x – y + z = 4
x – (1 – 4x +3z) + z = 4
x – 1 + 4x – 3z + z = 4
5x – 2z – 1 = 4
5x – 2z = 5
We now have two equations in two variables, which we can solve again by substitution.
–9x + 5z = 1
5z = 1 + 9x
z = 
+ 
x = 0.2 + 1.8x
Then,
5x – 2z = 5
5x – 2(0.2 + 1.8x) = 5
5x – 0.4 – 3.6x = 5
1.4x = 5.4
x = 
Now we can find y and z using the equations we were given or that we derived:
5x – 2z = 5
5
– 2z = 5
2z = 
– 5 = 
z = 
x – y + z = 4
– y + 
= 4
y = 
+ 
– 4 = 7
Let's check by trying the result 
in one of the original equations:
–x + 2y – z = 3
–
+ 2
– 
= 3
–
+ 14 – 
= 3
3 = 3
The solution checks out. For the sake of certainty, you can also check the solution using the other two equations.
Obviously, the substitution method is tedious, and it becomes more so very quickly as the number of variables in the problem increases. You can use other methods to solve such problems, but (as mentioned previously) some of them would require an entire course to flesh out adequately. Nevertheless, the substitution method is perhaps the most lucid method for learning how to solve these types of problems.
Practice Problem: Graph the expression z = 2x – y + 1.
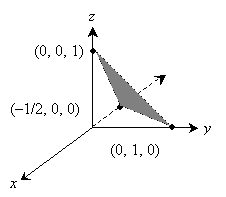
Solution: The expression given in the problem is a linear equation relating three variables: x, y, and z. From the lesson, recall that this expression corresponds to a plane, and we can plot it by finding the intercepts and then connecting them. We can calculate the intercepts by setting any two of the variables equal to zero.
z = 2(0) – 0 + 1 = 1 → (0, 0, 1)
0 = 2x – 0 + 1 = 2x + 1 → x = 
→ (
, 0, 0)
0 = 2(0) – y + 1 = –y + 1 → y = 1 → (0, 1, 0)
Use these points to plot the plane using an aspect drawing.
Practice Problem: Solve the following system of equations:
x + y = 3
2x – y = –1
Solution: We can use substitution to solve this problem. Let's take the first expression and solve for y.
x + y = 3
y = 3 – x
Now, substitute this result into the second equation and solve for the remaining variable.
2x – (3 – x) = –1
2x – 3 + x = –1
3x – 3 = –1
3x = 2
x = 
Use this result to find y.
y = 3 – x = 3 – 
= 
Thus, the solution in (x, y) form is 
. We can check the result by substituting these numbers into either or both of the original equations.
x + y = 3 = 
+ 
= 
= 3
The solution checks out.
Practice Problem: Find the solution for the following system of equations:
x – y + 2z = 3
–2x + y – z = 1
x + 3y – z = 2
Solution: We can apply our method of substitution to this problem as well. Let's start by solving the first equation for x.
x – y + 2z = 3
x = 3 + y – 2z
Substitute this result into the other two equations:
–2x + y – z = 1
–2(3 + y – 2z) + y – z = 1
–6 – 2y + 4z + y – z = 1
–y + 3z = 7
and
x + 3y – z = 2
(3 + y – 2z) + 3y – z = 2
3 + 4y – 3z = 2
4y – 3z = –1
Use these two results to solve for z.
–y + 3z = 7
y = 3z – 7
4y – 3z = –1
4(3z – 7) – 3z = –1
12z – 28 – 3z = –1
9z = 27
z = 3
We can now work back to find x and y using expressions that we have already derived.
y = 3z – 7
y = 3(3) – 7 = 9 – 7 = 2
x = 3 + y – 2z
x = 3 + 2 – 2(3) = 3 + 2 – 6 = –1
The solution is thus (–1, 2, 3). Again, you can check the result using any or all of the given equations (the solution must satisfy them all, however, to be legitimate).
