Objectives

Let's Begin!

One of the assumptions of ANOVA, which we discussed in the previous article, is that the samples in the data set are independent. But what if we want to consider a fixed set of samples over different conditions? For example, we might wish to test the effects of different dosages of a drug on a small group of patients. In this case, we have a fixed set of samples (the patients) and multiple conditions (the drug dosages). We could still be considering only one factor (say, for instance, a blood parameter or other medical effect), meaning that we would remain in the realm of one-way ANOVA. Nevertheless, because each patient contributes multiple data values to the overall data set, the assumption of independence for ANOVA is violated. We will now consider how we can deal with this situation by adjusting the F statistic.

Repeated Measures Design

The drug experiment situation described above is an example of a repeated measures design (or simply repeated measures). Because repeated measures typically involves a set of subjects (for instance, the patients in the drug experiment) that are tested over multiple conditions, repeated measures designs are also sometimes called within-subjects designs. Let's consider our medical example in more detail.

A physician is testing different dosages of a drug to determine if varying the dosage has a statistically significant effect on a particular medical parameter (which might be the level of a certain chemical in the blood, for instance). To this end, the physician recruits five volunteer patients who agree to take different dosages of the drug and then submit to tests of the parameter under examination. The physician carefully selects three different drug dosages (D₁, D₂, and D₃) and administers each to the patients, allowing sufficient time between dosages to allow the effects of the previous dosage to wear off. (One of the dosages might, for a control value, be a placebo.) For the patients labeled 1 through 5 for anonymity, the data set might look like the following.

To determine whether the means of each data column (group) differ significantly (potentially indicating that different dosages of the drug have some effect), the physician might be tempted to simply use one-way ANOVA. To be sure, the data involves more than two groups but only one factor, meaning that ANOVA would appear, on the surface, to be a legitimate way of analyzing the data. Nevertheless, because the ANOVA assumption of independent samples is violated in this case, we must use a slightly more sophisticated approach, which we call repeated-measures ANOVA (or within-subjects ANOVA).

The hypothesis testing procedure for one-way repeated measures ANOVA is the same as that for standard one-way ANOVA; the only difference is how we calculate the F statistic. Since the assumption of sample independence does not apply in repeated measures designs, we must modify the F statistic to account for the dependence among samples. We do not, in this article, provide an in-depth derivation of the F statistic for repeated measures design, nor do we go into all the details of the considerations that go along with using repeated measures ANOVA. Our discussion in this article, however, illustrates how care is needed when using ANOVA or any other statistical test, and it lays a foundation for further study of the different types of ANOVA, including the various types of repeated measures ANOVA and how they are to be understood.

The F Statistic for Repeated Measures ANOVA

As with standard one-way ANOVA, we define the mean of a measure (or column, following the example table arrangement above) j as and the grand mean of all the data values as . We also are interested in the mean for each subject (or row, again following the example table) in the data set-we'll call this mean for subject i. We'll assume that we have k measures (or columns) and n subjects (or rows). (In our example above, the data has three measures and five subjects.)

We can define the variation between measures as follows (this formula is analogous to the variation between groups for standard one-way ANOVA). Note that this is not a variance, since it is just a sum of squares.

We also define a variation between subjects, which has the same form as the variation between measures but involves the subject means rather than the measure means.

We can also define two new variations (or sums of squares): one for the total variation and one for the residuals, which simply involves the difference between the total variation and the between-measures and between-subjects variations. The total variation is the following:

The residual variation is the following difference:

We can convert these variations into variances (technically, mean squares) by dividing each expression by its corresponding number of degrees of freedom. For the between-measures variation, we have k - 1 degrees of freedom. Likewise, for the between-subjects variation, we have n - 1 degrees of freedom. These two cases follow the same pattern as the sample variances we have discussed in past articles. In the case of the total variation, we have nk - 1, since we are dealing with nk data values and only one mean value-the grand mean. The number of degrees of freedom for the residual variation is the difference between the total and between-subjects and between-measures degrees of freedom: this expression turns out to be (n - 1)(k - 1). The variances corresponding to the above variations are then the following.

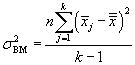
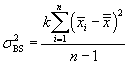
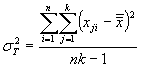
We can now define the F statistic for the case of one-way repeated measures ANOVA.

Note that the numerator has k - 1 degrees of freedom, and the denominator has (n - 1)(k - 1) degrees of freedom. This information is important for finding the critical value in the Ftables. (We use the same tables for the F-test in this case as we do in the case of standard one-way ANOVA.)

Limits of Repeated Meas   ures ANOVA

As with any statistical tool, care must be taken when using repeated measures ANOVA. Several factors must be considered when interpreting data for a particular experiment. For instance, in the medical experiment example discussed above, administration of a dose of the drug could cause lasting effects that influence a patient's response to later dosages. Thus, although the physician might go to great lengths to ensure that each dose is administered to a patient with a "clean slate," so to speak, the conditions of the experiment for a particular patient could change as the experiment progresses. Also along these lines, the patient could be under outside influences that affect the measurements for the drug. These and other considerations can have a serious impact on a repeated measures design, so this kind (or any kind) of statistical analysis must not be undertaken blindly. Mathematics is critical to statistics, but the key to a good statistical analysis is proper interpretation of the math in light of the numerous factors that bear on it.

The following practice problem continues with our medical experiment example from above and illustrates how repeated measures ANOVA can be used in a practical case.

Practice Problem: Using the medical example data from above, determine if the drug dosages have a statistically significant effect (to a significance level of 0.01).

Solution: Because the samples are not independent, the physician can use repeated measures ANOVA to determine if different dosages of the drug produce a statistically significant effect. The problem assumes a significance level of 0.01. The null hypothesis is that the means of the measures do not vary significantly. We can calculate the value of F as follows, starting with the various means. (The dosage-or measure-means are calculated first, followed by the patient-or sample-means and then the grand mean.)

Using these means, we can calculate the required variations (sums of squares) as follows. Again, we do not include all the details of these calculations-only the results. If you are unsure how to perform the calculations, see the numerous examples in previous articles. Note that k = 3 and n = 5 for this case; furthermore, j corresponds to the index of the drugs (D_j) and i corresponds to the patient index (or number).

We can now calculate the necessary variances (mean squares) for use in the F statistic.

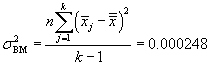
The value of F is then

Let's now find the critical value for the F-test. The numerator of F has two degrees of freedom, and the denominator has eight. Our significance level is 0.01. Thus, the critical value is

Thus, since F > c, we are justified in rejecting the null hypothesis. The physician therefore can conclude that the drug has some significant effect on the patients.