We can calculate the acceleration of objects resulting from any number of forces acting on them. We exemplify our mathematical tools by looking at weight (gravitational force) and the normal force.
Key Terms
o Mass
o Newton's second law of motion
o Newton (unit of force)
o Weight
o Gravitation
o Newton's third law of motion
o Normal force
Objectives
o Express vectors algebraically as the sum of two component vectors
o Recognize the importance of carefully using units when solving physics problems
o Use Newton's second and third laws of motion to find the acceleration of an object when various forces are applied to it
Let's Begin!
In this article, we will consider Newton's second law of motion, which relates the net force to the mass and acceleration of an object, and Newton's third law of motion, which expressed the relationship between two objects and the force exerted between them. To begin, we first consider another way to express a vector; this time, instead of using the coordinate pair (x, y) to express the vector, we use an algebraic expression in terms of unit vectors.
Expressing Vectors Algebraically
We can divide a vector into its component parts in the x and y directions; furthermore, we can take each component and write it in terms of a magnitude and a unit vector in either the x or y direction. The unit vectors are (1, 0) in the x direction (we can call this unit vector x) and (0, 1) in the y direction (we can call this unit vector y). Thus, for instance, we can write (3, 4) as 3x + 4y. Note that we can show this method works by using our coordinate representation of vectors:
3·(1, 0) + 4·(0, 1) = (3, 0) + (0, 4) = (3, 4)
Note, however, that we treat a vector as a variable when performing algebraic manipulations; in other words, we can only add like kinds (just as we can only add coordinates corresponding to the same direction). Thus, if we want to add two vectors expressed as 2x – 4y and –x + 3y, the result is the following.
(2x – 4y) + (–x +3y) = (2 – 1)x + (–4 + 3)y = x – y
Practice Problem: If A = 2x – y, B = –4x + 2y, and C = x – 3y, find A – C + B.
Solution: Simply use our algebraic approach to adding and subtracting the components of the vectors as shown below.
A – C + B = (2x – y) – (x – 3y) + (–4x + 2y) = (2 – 1 – 4)x + (–1 + 3 + 2)y
A – C + B = –3x + 4y
The Importance of Units
Before we take a look at the relationship between force and acceleration according to Newton's second law of motion, it behooves us to first recognize the importance of units in physics problems. Force, acceleration, mass, and so on are not just pure numbers: they require corresponding units to provide a point of reference for making them meaningful. For instance, if someone caught a large fish and simply said it had a length of 6, we would have trouble determining exactly what the fisherman means--6 inches? 6 feet? But if the fisherman says the fish was 6 feet long, then we know what he means because he has provided a unit with the number. Indeed, he caught a big fish! Likewise, physical quantities must always be expressed in terms of some standard--a unit--that makes the number meaningful in a physical context. For our purposes, we will rely primarily on the metric system of units (sometimes called SI units). In our study of motion, we will use the kilogram as our standard unit of mass, the meter as our standard unit of length, and the second as our standard unit of time. Units of velocity, acceleration, force, momentum, and energy can all be expressed in terms of these three basic units.
Newton's Second Law of Motion
Imagine that you are trying to move two different objects, one of which is light and the other heavy (that is, one has a small "mass" and the other has a large "mass"). Obviously, you will need to exert yourself more (that is, apply more force) to move the heavy object than to move the light object. If you apply a particular force F to the light object, it will start accelerating at one rate; if you apply the same force F to the heavy object, it will accelerate at a slower rate. (Another way of looking at the situation is that if one person applies force F to a light object and another person applies force F to the heavy object, then the person with the lighter object will get his object moving faster in less time than will the other person with the heavy object.) We can thus think of the mass of an object as its resistance to acceleration: the more massive it is, the more force is required to achieve a certain acceleration. Newton's second law of motion summarizes these concepts in the following mathematical expression.
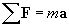
In this expression,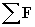 
is the vector sum of the forces on the object--in other words, it is simply the net force (a value we already know how to calculate). The factor m is the mass of the object, and the vector a is the acceleration (note again that acceleration has both a magnitude and a direction). Acceleration, once again, is the time rate of change of the velocity. Velocity has units of meters per second (m/s); acceleration thus has units of meters per squared second (m/s2). Let's consider a unit analysis of the expression above to determine the units associated with force (we look only at magnitudes; the unit vectors x and y are unitless quantities).
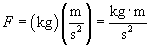
Units of kilogram meters per squared seconds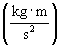 
are also called newtons (N); in other words,
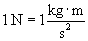
The following practice problem applies these unit concepts along with vectors and Newton's second law.
Practice Problem: The following forces (expressed in newtons) act on an object of mass 20 kilograms: 3x + 2y, –4x + y, x – 5y. What is the acceleration of the object? What is the magnitude of the acceleration?
Solution: To solve this problem using Newton's second law of motion, we need to find the net force by adding each of the force vectors:
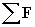= (3x + 2y) + (–4x + y) + (x – 5y) = (3 – 4 + 1)x + (2 + 1 – 5)y = –2y N
Now, let's use Newton's second law of motion to find the acceleration of the object. Note that the problem statement tells us that the object's mass is 20 kg.
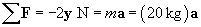
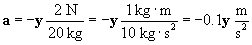
Since the acceleration is purely in the negative y direction, its magnitude is simply –0.1 meters per squared second.
So, what is an example of a particular force that we might encounter in physics problems (and real life)? One such force is weight (not to be confused with mass--an astronaut in orbit around the Earth has zero weight, but he still has the same mass!). Objects with mass attract one another; we call this gravitation. If we were to drop an object and measure its acceleration anywhere on the Earth, we would find that it is 9.8 m/s2 in the downward direction (this is often written simply as g or the vector g). Let's apply Newton's second law; for an object of mass m, we'll call the force Fg. Assuming no other forces are acting on the object and the downward direction has a unit vector –y,
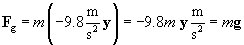
Newton's Third Law of Motion
If an object is released in midair, it falls; if it is set on a solid surface such as a table, however, it remains motionless. Thus, we might wonder what is happening to counteract the force of gravity. We can easily note that regardless of the mass of the object (within the strength limits of the table), the table holds it up, apparently by exactly countering the force of gravity! Newton's third law of motion addresses this situation. You may have heard the expression that "an action has an equal and opposite reaction"; in physics, this simply means that given two objects A and B, the force that B exerts on A (which we can call FBA) is equal and magnitude and opposite in direction to the force that A exerts on B (FAB). Thus, we can write the following expression of Newton's third law.
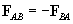
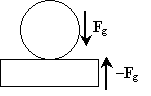
Thus, the table exerts a force on the object equal and magnitude and upward in direction, thus counteracting the force of gravity. The object therefore experiences no acceleration. The force exerted by the table on the object is called the normal force (because it is directed normally--or perpendicularly--to the surface of the table at the point of contact).
Practice Problem: An box of mass 10 kg rests on a cart whose wheels are frictionless. If a woman pushes on the cart with a force of 100 N in the horizontal direction, what is the acceleration of the cart?
Solution: Apply Newton's second law of motion to solve this problem. The problem statement tells us that the mass is 10 kg and the force applied by the woman is 100 N. Let's make a diagram of the situation.
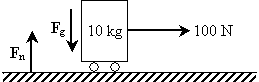
The normal force, Fn, balances the weight of the cart, Fg (Newton's third law); thus, the net force on the object is 100 N in the horizontal direction (we'll call it the positive x direction--the corresponding unit vector is then x). Now, we apply Newton's second law.
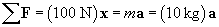
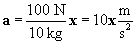
Thus, the acceleration is 10 meters per squared second in the same direction as the force (horizontal).
Practice Problem: For the situation described above, what is the acceleration if she pushes with the same force directed 30° measured up from horizontal?
Solution: Let's redraw the situation.
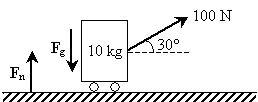
The force that the woman exerts has two components; using trigonometry, we can write the force vector Fp as the sum of a force in the horizontal direction (x) and the vertical direction (y).
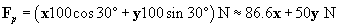
The vertical component of the pulling force reduces the downward force on the object somewhat (the weight of the object is 98 newtons); the normal force, however, adjusts and is still equal in magnitude and opposite in direction (the normal force in this case is 98 – 50 = 48 newtons). Thus, the net force is simply the horizontal component of the pulling force. The acceleration is then the following.
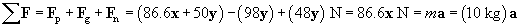
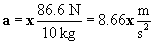
Thus, the acceleration in this case is 8.66 meters per second squared in the x direction--slightly smaller than in the case of the previous problem.
Various other types of forces can also be analyzed using these laws of motion; although we do not discuss them here, the mathematical techniques that we have studied here can be used to solve a much wider variety of problems.
