In this article, we'll review potential energy and its relationship to kinetic energy through the concept of mechanical energy. In addition, we look at power, which is energy supplied over some interval of time.

Key Terms

o         Potential energy

o         Mechanical energy

o         Gravitational potential energy

o         Conservation of energy

o         Dissipation (of energy)

o         Elastic potential energy

o         Power

o         Watt

Objectives

o         Understand the concept of potential energy and its relationship with kinetic energy

o         Know why mechanical energy is conserved (in a frictionless environment)

o         Define the power supplied when doing work on an object

Let's Begin!

Potential and Mechanical Energy

In this article, we'll review the concepts of potential energy and power. For instance, consider a ball suspended some height h above the floor. If that ball is released, it will gain kinetic energy because of the gravitational force. You might wonder where exactly this energy is coming from--certainly, if we could create energy out of nothing, we could solve many of the problems that currently plague our world! Nevertheless, we find in the world that we don't get more energy out of a system than has been put into that system (whatever the source). The situation of the ball is no different. When someone puts work into lifting the ball, he is increasing the ball's potential energy, which in some sense is mechanical energy (or energy of motion) stored in the object. Thus, the work done on the ball does not go into oblivion--it becomes "stored" energy (in this case, in the form of gravitational potential energy). When the ball is released, the stored potential energy becomes kinetic energy. In fact, all of the work done in lifting an object to a height h becomes kinetic energy once that object falls back to its original height (in this case, a height of zero).

Note that the kinetic energy of the ball cannot exceed the potential energy when the ball is released (of course, this only applies to the ball between its initial and final heights); in fact, the change in kinetic energy is equal in magnitude to the change in potential energy. Again, the work done on an object in lifting it a height h becomes kinetic energy when that object falls back to its original height. We can therefore write the following expression, where K is the kinetic energy and U is the potential energy.

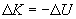
This is simply a mathematical way of saying that the kinetic energy increases as the potential energy decreases, and vice versa. We can also note the following by rearranging this expression slightly.

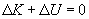
In other words, the in the kinetic energy must always balance the change in potential energy. If we define the total mechanical energy E as the sum of the kinetic energy (K) and the potential energy (U), then the total change in mechanical energy, ?E, is the following.

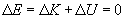
In other words, mechanical energy is conserved (neither created nor destroyed); we call this concept conservation of energy. This conservation of mechanical energy actually applies only in the ideal case where friction (in all its forms) is neglected. For instance, if we allowed a block to slide down a ramp, such as is shown below, we would find that the block would eventually come to a stop.

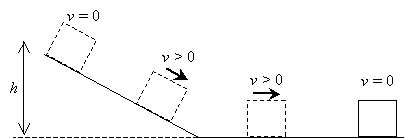
Even though the block has a potential energy mgh (where m is the mass of the block) at the top of the ramp, the block loses velocity and eventually comes to a stop somewhere on the flat surface. If mechanical energy were conserved perfectly, the block should just continue on with a certain kinetic energy (speed). Nevertheless, friction causes the block to dissipate its mechanical energy in the form of heat. (Note that your hands warm up when you rub them together!) Thus, in reality, mechanical energy is not conserved. In cases where friction can be ignored, however, we can assume that mechanical energy is conserved to help us solve problems.

Practice Problem: A skier is trying to break a speed record of 35 meters per second on a certain slope. With his skis and other equipment, the skier has a mass of 90 kilograms. At the bottom of the slope is a level (that is, horizontal) area where the skier's speed is measured. Assuming friction and air resistance are negligible and assuming the skier does not give himself a "push" at the start, at what minimum elevation above the level area must the skier start at to have a chance at breaking the speed record?

Solution: To gain speed, the skier relies on conversion of gravitational potential energy into kinetic energy as he goes down the slope. Thus, we need to first calculate the required kinetic energy for him to break the speed record. We can then convert this to gravitational potential energy to find the minimum elevation from which he must begin his descent.

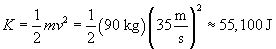
In a frictionless environment, mechanical energy is conserved. Thus, the skier needs at least 55,100 J of gravitational potential energy to break the speed record of 35 m/s. This potential energy U is equal to mgh, where m is the skier's total mass, g is the acceleration due to gravity, and h is the vertical elevation. Because we know g and m, we can set mgh equal to the required kinetic energy of 55,100 J and then calculate the minimum elevation, h.

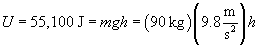
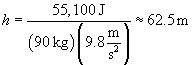
Thus, the skier must start from an elevation of greater than 62.5 meters to have a chance at breaking the speed record (in a frictionless environment--he must also ski flawlessly!).

Springs: Mechanical Energy Illustrated

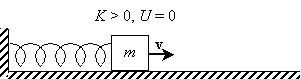
One example of the interplay of potential and kinetic energy is a spring. If compressed, a spring will tend to push back with a certain force that attempts to restore the spring to its original size. If expanded, the spring will tend to pull back with a similar restoring force. Imagine a spring that is parallel to a horizontal surface and that is attached to a block of mass m, as shown below. The spring is relaxed, meaning that it is neither compressed nor extended. We define right as the positive x direction.

Alternatively, if we push the block, causing the spring to expand, the spring then exerts a restoring force F_r in the negative x direction.

Now, let's imagine that we either stretch (expand) or compress the spring and then release it. For the sake of example, we'll say we start by compressing the spring (it makes no difference, however). In the instance that we release the block, it has zero velocity, but a force is acting on it, causing it to accelerate. Thus, the block has no kinetic energy, but it does have potential energy (specifically, elastic potential energy).

Once the spring returns to its "relaxed" position, it no longer applies a force to the block. The block, however, has had all its elastic potential energy converted to kinetic energy; its momentum causes it to extend the spring, which then converts the blocks kinetic energy back into potential energy.

Calculation of the exact potential energy of a block on a spring using Hooke's law (a model for the restoring force of a spring) requires integral calculus, so we will not pursue the topic further. Nevertheless, we are still able to draw conclusions about this situation based on what we know about the conservation of mechanical energy, as we will see in the following practice problem.

Practice Problem: A 3-kilogram block is attached to a spring on a horizontal, frictionless surface. The spring is compressed and the block then released. The maximum speed of the block is measured at 2 meters per second. What is the elastic potential energy of the block when the spring is fully extended?

Solution: We know that mechanical energy is conserved in the frictionless case. Thus, the total mechanical energy of the spring and block at the point of release (after the spring is compressed by some force) must always be constant. Let's call this constant E. When the block is released, it initially has zero velocity, meaning that all the mechanical energy is (elastic) potential energy, or U = E.

All of the elastic potential energy becomes kinetic energy when the spring reaches its relaxed position. This is also the point at which the block has a maximum speed, because K = E. Let's now calculate K for this case.

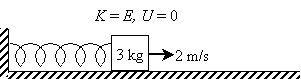
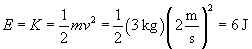
When the spring is fully extended, the block is at rest (that is, it has zero velocity) and all of the kinetic energy has once again become elastic potential energy, meaning that U = E.

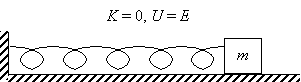
But because we know what E is from above (and from the conservation of mechanical energy), we know that U = 6 J when the spring is fully extended.

Power

Energy is not the only consideration when dealing with motion. For instance, an economy car and a sports car might have about the same mass and might be able to both reach a certain (moderate) speed v (and therefore a certain kinetic energy K). Nevertheless, the engine of the sports car is likely able to accelerate the car faster than can the economy car. In other words, the sports car's engine is able to supply more power, or more energy per unit time. We can therefore define the average power P as the work W done on an object (in our example, done by the engine on the car) divided by the time span ?t.

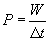
Note that we earlier defined work as the scalar product of the applied force and the displacement vector. Thus,

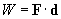
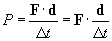
But the displacement d divided by the time ?t is simply a velocity. Thus we see that power can be more generally defined as follows, where v is the velocity of the object to which the force F is being applied.

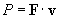
Note that power has units of joules per second, which is the same as a watt (W).

Practice Problem: A winch is being used to lift a 200-kilogram piano off the ground to a height of 30 meters. If the winch lifts the piano at a constant velocity of 0.25 meters per second, how much power must it be able to supply?

Solution: We can approach this problem in any of several ways. Let's try calculating the work done on the piano by the winch and then the time required to lift the piano. We can then use the following power formula presented earlier:

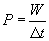
The work done on the piano by the winch is the product of the piano's weight and the displacement (distance) lifted (the applied force and the displacement vector are parallel).

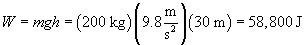
Now, let's calculate the time ?t required to lift the piano.

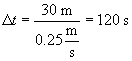
We can now calculate the power that is required from the winch.

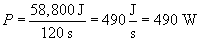
Thus, the winch must supply a power of 490 watts.