Key Terms
o Circle
o Radius
o Diameter
o Arc
o Subtend
o Sector
o Chord
o Secant
o Tangent
o Circumference
Objectives
o Know how to fundamentally define a circle
o Identify various parts of circles
o Calculate the area and circumference of a circle or portion thereof
Introduction to Circles
A circle is simply a figure defined by all the points that are equidistant from a given center point. Thus, we can define a circle (without a definite location) by specifying the distance from the center; alternatively, we can define a circle (with a definite location) by specifying the distance from and the location of the center. The distance from the center of the points that lie on the circle is called the radius (plural radii) of the circle. A circle with a radius r and center point C is shown below.
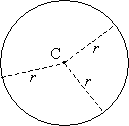

Note that regardless of which point on the circle is chosen, it is always a distance r from the center point, C. Each of the line segments drawn from C to the circle is called a radius (in other words, no one segment is defined as the radius, since all such segments are equal in length). The circle itself does not show any angles or sides that we can use to determine how many degrees are in the figure (as we did with polygons), but we can see that any two radii do form an angle α, as shown below.


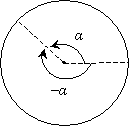
Using our measurement of degrees, this angle α can (unambiguously) be any value between 0° and 360°. We can also define angles with either positive or negative numbers, depending on the direction of measurement from a particular radius--a positive angle is traditionally measured in the counterclockwise direction, and a negative angle is traditionally measured in the clockwise direction, as shown below.

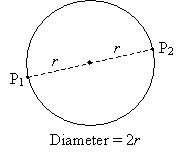
We can also identify other parts of a circle. Given any point P1 on the circle, the most distant point P2 that is also on the circle is on the exact opposite side, and these points are the length of two radii apart. The line segment that connects them passes through the center and is called the diameter of the circle.

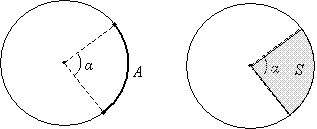
Any two radii in the circle (which form an angle α), such as those shown below, form an arc and a sector. The arc is the portion of the circle opposite to (or subtended by) the angle α and between the endpoints of the radii. The sector is the area enclosed by the arc and the radii. The arc A in the diagram below is shown as a bold line, and the sector S is shown as a shaded area.

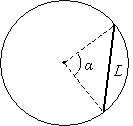
Any line segment connecting two points on the circle is called a chord. Note that a diameter is a chord (the longest possible chord of a circle!). The chord D is shown below as a bold line.

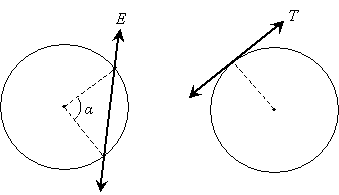
Other special figures related to circles are secants and tangents. A secant is simply a line that intersects two points of the circle (a chord is a segment of a secant). A tangent is a line that intersects the circle at exactly one point. Secant E and tangent T are shown in the diagram below as bold lines.

Practice Problem: Identify each part (labeled A through E) of the circle below.
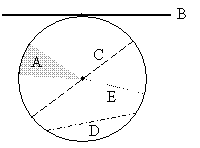

Solution: Each portion of the circle or other line can be identified by its relationship to the entire circle. Each of these figures is discussed and defined above. The shaded area A is a sector. The line (or line segment) B is a tangent (note that it intersects the circle at only one point). C is a diameter, D is a chord, and E is a radius.
Basic Characteristics of Circles
Now that we have identified some of the components of circles, we can now begin to derive some of their characteristics using the tools we have developed thus far. Some of the properties of circles require trigonometry to derive (such as the length of a chord subtended by an angle α), but others we can derive or simply state basic formulas that we can use to solve problems. Let's start with the circumference and area of a circle. The circumference of a circle is simply the length of the boundary (that is, the perimeter) of the circle. We will simply state the formula for the circumference C of a circle in terms of the radius (r) or the diameter (d):
C = 2πr = πd
Note that with the formula for the circumference, we introduce the number π. Because π is (most mathematicians think) an irrational number, we cannot write it out exactly in its decimal form, nor can we write it exactly as a fraction. We can, however, write a decimal estimation of π that is sufficient for our purposes.
π ≈ 3.1416
Many calculators have a built-in key for the number π (although the calculator still just uses an approximation of π). For many calculations, an approximate π value of 3.14 yields sufficient accuracy. As it turns out, π also appears in the formula for the area of a circle. Let's write the area A in terms of the radius r.
A = πr2
Note again that we have not really derived these formulas; we are simply stating them as fundamental facts upon which we will base the rest of our investigation of the characteristics of circles.
Practice Problem: Find the area and circumference of a circle with a diameter of 4 inches.
Solution: One of the first rules of solving these types of problems involving circles is to carefully note whether we are dealing with the radius or the diameter. In this problem, the circle is described using the diameter, which is 4 inches. The radius is thus 2 inches. Let's now calculate the area A and circumference C using the formulas given above.
A = πr2 = π(2 in)2 ≈ (3.14)(4 in2) =12.56 in2
C = πd = π(4 in) ≈ (3.14) (4 in) = 12.56 in
Coincidentally, the area and circumference have the same numerical values (but not the same units!). This is not generally the case, of course.
Let's take a look at the characteristics of other parts of a circle. For instance, now that we know how to calculate the circumference of a circle, we can also calculate the length of an arc (which is simply a portion of the circumference). An angle α defined by two radii subtends an arc. Let's take a look at several examples, from which we can identify a pattern. The arc K in each case is shown as a bold curve. The circumference of the circle is C.
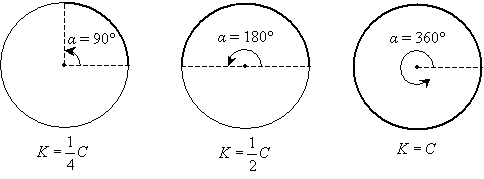
The expressions under each example can be derived by inspection. We know that if the angle α is 90° (one-quarter of the full 360° of the circle), then the subtended arc is one-quarter of the circumference. The same reasoning applies to determining the arc length K for the other two cases as well. Thus, we can see that the arc length is related to the circumference as the angle α is related to 360°. But this is simply a ratio that we can write as follows.
![]()
![]()
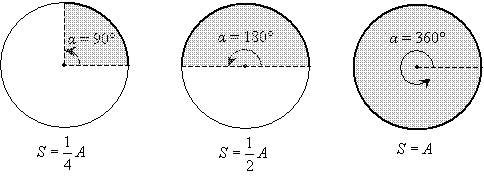
Thus, the area of sector S is related to the area A according to the ratio of α to 360°. We can once again derive a formula.
![]()
![]()
Practice Problem: A central angle γ in a circle of radius 10 units forms a sector with an area of 2.62 square units. Find the measure of γ.
Solution: Let's start by drawing a diagram of the problem. This diagram need not be to scale-we can simply use it to more easily identify the parts of the circle discussed in the problem. We'll call the sector S, and we know S = 2.62 units2.
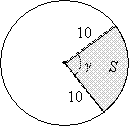

We can use the formula presented earlier to relate the area S of the sector to the area A of the circle.
But we also know how to calculate A using the given radius of 10 units.
A = πr2 = π(10 units)2 ≈ 3.14(100 units2) ≈ 314 units2
Now let's find γ.
![]()
![]()
![]()
Thus, the angle has a measure of 3°.