Introduction
In this article, we take only a brief qualitative look at factor analysis, which is a technique (or, rather, a collection of techniques) for determining how different variables (or factors) influence the results of measurements (or measures).
Key Terms
o Factor analysis
o Exploratory factor analysis
o Confirmatory factor analysis
o Factor loading
Objectives
o Recognize some of the key terms associated with factor analysis
o Understand the overall purpose and procedures of exploratory and confirmatory factor analysis
Let's Begin!
We have focused primarily on quantitative, mathematical techniques for analyzing sets of data. We have studied typical descriptive statistics, multivariate data, cross tabulations, correlation, regression, and various types of hypothesis tests. These subjects require a fair amount of sometimes tedious math. We now turn to an overview of another topic: factor analysis. In this case, unlike in most of our previous articles, however, we will only discuss the subject qualitatively, providing simply an overview. Factor analysis is a complicated topic that is subject to many subtleties, and although it has a number of mathematical aspects, we will largely avoid these for lack of time.
Purpose of Factor Analysis
Given a set of measured values (such as, for instance, the income and age of a group of employees at a particular company), factor analysis seeks to apply statistical methods to the problem of determining how underlying causes influence the results. Factor analysis methods are sometimes broken into two categories or approaches: exploratory factor analysis and confirmatory factor analysis. The first, exploratory factor analysis, focuses on determining what influences the measured results and to what degree they are doing so. The second, confirmatory factor analysis, focuses on determining whether a particular group of factors influences the data in an expected manner. Thus, these two divisions of factor analysis have two different goals and, correspondingly, two different general approaches to their respective problems.
Exploratory factor analysis attempts to determine what factors have a bearing on a particular measure (such as age or income, following the above example) and how strongly those factors influence the measure. Exploratory factor analysis can be useful in cases where, for example, a researcher wishes to determine what has the greatest influence on a particular measure. The researcher might find, again following our above example, that employee income is most greatly influenced by the number of years the employee has worked at the company and by how many years of higher education the employee has.
Confirmatory factor analysis looks at a factor model and determines how well it matches with observed data. Thus, confirmatory factor analysis is more of a "testing" procedure, whereas exploratory factor analysis is more of a "development" procedure. Confirmatory factor analysis can be used, for example, to evaluate a given factor model--in a medical situation, this might involve confirming a model designed to predict whether a drug will have certain effects on the basis of certain medical factors of a patient.
Illustrating a Factor Model
Factor models that are to be used in confirmatory factor analysis or that are developed by way of exploratory factor analysis can be illustrated using a path diagram. Factors are often represented as circular blocks, whereas variables (or measures) are represented by square blocks. A hypothetical path diagram illustrating a factor model is shown below. Factors F1 through F3 influence variables X1 through X5, with the path labels indicating the strength of the relationship between the factor and the corresponding variables.
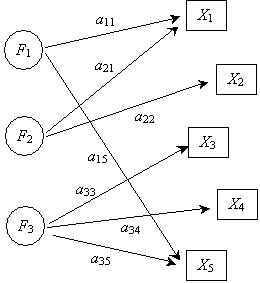

Thus, a set of variables (or measures) may have a number of factors that influence their values. The factor model path diagram helps illustrate and clarify these relationships.
Factor Analysis Procedure: Overview
Again, we will not go into the specific mathematical details of how to perform an exhaustive factor analysis--such details are beyond the scope of this article. First, we consider a basic procedure for exploratory factor analysis.
The first step of exploratory factor analysis is to collect the necessary data for the variables of interest in the investigation. The next step is to construct the covariance matrix for the variables. The covariance matrix can easily be converted to a correlation matrix by noting that the correlation coefficient is a normalized form of the covariance--for instance, the covariance ![]() for variables X and Y can be converted into a correlation value by dividing by the product of
for variables X and Y can be converted into a correlation value by dividing by the product of ![]() and
and ![]() . The covariance (or correlation) matrix describes how the variables are interrelated.
. The covariance (or correlation) matrix describes how the variables are interrelated.
The next step is to decide how many factors will be included in the analysis-this number is less than the total number of variables. Effectively determining this number may require a theory that describes the relationships between factors and measures prior to the analysis. Following this step, the factor loadings must be calculated--these are the values that quantify the strength of the relationship between a factor and a measure. The factor loadings are the a values in the path diagram; thus, they are analogous (and are sometimes considered to be the same as) standardized regression coefficients. Calculating the factor loadings is a complicated task that is typically left to a computer, especially when the data sets are large. (In this article, we deal primarily with small data sets for which computations can easily be done by hand. In real-world situations, the data sets are often much larger.) Finally, the results of the factor analysis must be properly interpreted. Such interpretation depends largely on the details of the problem.
For confirmatory factor analysis, the procedure is similar to that of exploratory factor analysis up to the point of constructing the covariance (or correlation) matrix. At this point, confirmatory factor analysis diverges: the next step is to fit the collected data to the model and then determine whether the model correctly describes the data. If so, then the model may be tested in other situations or applied to a new situation. Otherwise, the model must be re-evaluated.
More Information on Factor Analysis
Because of the complexity of the topic, as mentioned above, we have only discussed factor analysis in the broadest of terms. Nevertheless, extensive information is available on the Internet that provides further details about the intricacies of factor analysis. See the resources included with this article for more information about this subject.
Practice Problem: How might one determine if the results of a factor analysis fit a set of measured data?
Solution: In the article, we noted that that the factor loadings, which are calculated as part of exploratory factor analysis, can be interpreted as the standardized regression coefficients. As a result, we can use these coefficients to form a regression equation, which we can then compare with the measured results. If the regression results are not a good match with the observed results, then we can conclude that the factor model is not a good fit to the data in that case.