Introduction
In this article we will review the physics behind the electric force. For simplicity, we only consider the case where all charged objects are stationary. We study how to calculate the force on a charged particle resulting from one or more additional charged particles.
Key Terms
o Electrostatics
o Electric charge
o Coulomb
o Coulomb's law
o Principle of superposition
Objectives
o Recognize and be able to use Coulomb's law to calculate the magnitude and direction of the force of one charged particle on another
o Calculate the magnitude and direction of the net force on a charged particle resulting from multiple additional charged particles
Let's Begin!
We now turn from Newtonian mechanics, which deals with the motion of objects under the influence of forces (or no forces), to the subject of electrodynamics, which deals with electromagnetic radiation (light) and its source. This topic, however, is not entirely divorced from what we have studied thus far; the same principles of motion apply. For our purposes, we simply focus more on a particular force--electromagnetism. Because this subject is vast and complicated, we will only touch on a few key points, but these concepts provide a foundation that will allow you to study the topic in greater depth.
Introduction to Electrostatics
If you've ever rubbed a balloon on your head, placed the balloon against a wall, and noticed that the balloon sticks, you have seen a phenomenon of electrostatics. Electrostatics is the study of stationary electric charges and the forces that arise from them. Electric charge is a property of matter that gives rise to attractive and repulsive forces. In some ways, electric charge is like mass: an object with mass exerts an attractive force on all other objects with mass. Whereas mass only ever exerts an attractive force on other masses, however, the electric force can be either attractive or repulsive. If, for instance, you were to take two balloons and rub them on your head, you would find that the balloons tend to repel one another if you bring them close. (The action of rubbing the balloon on your head deposits excess electric charge on the balloon.) Because the same action is performed for both balloons, we see that like charges tend to repel one another. By similar experiments, we can find that charge comes in two types, which (by convention) we label as "positive" and "negative." The SI unit of electric charge is the coulomb; to provide some point of reference, a single electron has a charge of about 1.6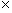
10-19 coulombs (C). You may also have heard of an ampere, which is the SI unit of current: one coulomb is the amount of charge that flows through a cross section of a current-carrying object (such as a wire) in one second.
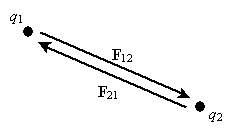
By carefully studying charge, one can experimentally derive Coulomb's law, which expresses the force between two particles (point-like objects) that have respective charges q1 and q2. The expression for F12 below is for the force of charge q1 on charge q2. By Newton's third law of motion, F21 (the force of charge q2 on charge q1) is simply –F12. The unit vector r12 is simply a vector of unit magnitude pointing in the direction of q2 from q1.
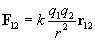
Note that the magnitude of the force between the two charges is proportional to the product of the charges (in coulombs) and is inversely proportional to the square of the distance between them. The unit vector r12 indicates that the force is directed from one charge toward another, making the force either attractive or repulsive in nature. Note also that if the two charges have the same sign (in other words, they are "like" charges), then they repel one another. If their signs are different, they attract one another. The factor k is simply a constant determined by the material in which the charges are located. In a vacuum (outer space is very close to being a vacuum), k is the following, where ?0 is 8.854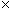
10-12 farads per meter (F/m). (We will not discuss the unit of farads, but suffice it to say that it acts in this context to produce units of newtons for the force F. One farad, then is one square coulomb per newton per meter: 
.)
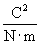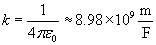
For all the problems in this article, we will simply assume that the charged particles are in a vacuum. Values of k for materials other than a vacuum can be found in (or derived from information in) various physics reference books.
As a side note, the gravitational force between two masses (m1 and m2) obeys a very similar expression, where G is the so-called gravitational constant (about 6.67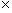
10-11 cubic meter per squared second per kilogram). The negative sign indicates that the force is always attractive (because the value of m is always positive).
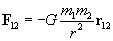
Practice Problem: A particle with a charge of 1 coulomb is four meters away from a particle with a charge of –4 coulombs. What is the magnitude of the force on the second charge, and is it directed toward or away from the first charge?
Solution: We can use Coulomb's law to solve this problem. Using the rules of vectors, we find that the magnitude of the force of the first charge (q1) on the second charge (q2) is simply the following:
We can plug in the appropriate values to calculate the force in newtons.
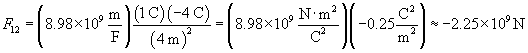
Note that the magnitude of the charge is tremendous--over one billion newtons! (As it turns out, the electric force is much stronger than the gravitational force.) Because the sign of the result is negative, the force on the second charge is toward the first charge. This answer makes sense, since unlike charges attract, as we discussed earlier.
Principle of Superposition
As it turns out, electric forces from different sources simply add as vectors; in other words, if we want to calculate the force on one charge from two other charges, we can simply add the individual force vectors. This ability to add forces in this simple manner means that the electric force obeys the principle of superposition; thus, we can simply add (or "superpose") electric forces to find the total force.
Practice Problem: A particle with charge 1 coulomb is located at the origin of a two-dimensional grid (divided into units of meters). If a particle of 2 coulombs is located at (1, 3) (in meters) and a particle of –4 coulombs is located at (–2, 5), what is the total force on the charge at the origin?
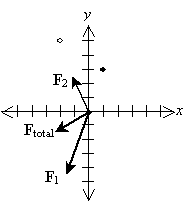
Solution: Let's draw a diagram of the situation so that we can clearly see the layout of the problem. This diagram will also help us to determine whether our solution makes sense. We draw the negative charge as an open circle and the positive charges as closed (filled-in) circles. We'll also identify the horizontal dimension as x and the vertical dimension as y.
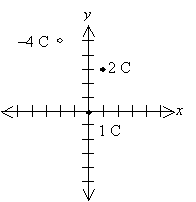
Let's calculate the force in each case. First, we'll consider the force of the 2-coulomb charge on the 1-coulomb charge, which we'll call F1.
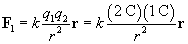
We must now calculate the unit vector r and the distance r between the charges. We can simply use the position of the 2-coulomb charge as its position vector relative to the origin: (1, 3), or x + 3y. The magnitude r of this vector is the distance between the particles (in meters).
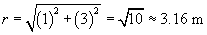
We can divide x + 3y by r to obtain a unit vector. This unit vector must be multiplied by –1 to get r in this case, because r should point from the 2-coulomb charge to the 1-coulomb charge. Note that r is unitless.
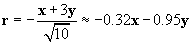
Now calculate the force of the 2-coulomb particle on the 1-coulomb particle.
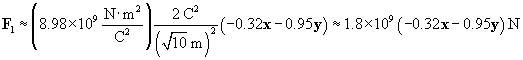
We can now use the same approach to calculate the force on the charged particle at the origin due to the –4-coulomb charge. We must calculate a new r and r, where the position vector of the –4-coulomb charge is (–2, 5). Once again, we negate the position vector to get r.
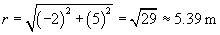
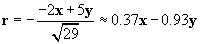
Let's now calculate the force of the –4-coulomb charge on the 1-coulomb charge (we'll call this force F2).
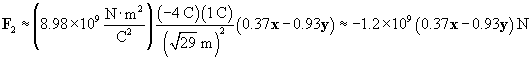
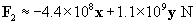
The total force on the charge at the origin is then F1 plus F2. We can also write the force in terms of a magnitude and a unit vector.
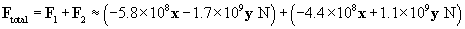
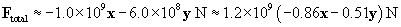
Let's show all the forces on the graph; the lengths of the vectors are roughly proportional to their respective magnitudes. Note that the directions of the forces make sense on the basis of what we have learned about vectors.
