Objectives
o Identify some critical steps of the process for solving practical geometry problems
o Apply geometry problem-solving techniques to practical situations
Geometry has a variety of real-life applications in everyday situations. In this article, we will learn to apply geometric principles and techniques to solve problems. The key to solving practical geometry problems is translation of the real-life situation into figures, measurements, and other information necessary to represent the situation conceptually. For instance, you already know how to calculate the area of a composite figure; if you were asked to determine how much floor space is available in a certain building with a composite shape, you would simply need to apply the same principles as you would use for calculating the area of a composite figure. Some measurements of the building might, of course, be required, but the same problem-solving techniques apply.
It behooves us to present a basic approach to solving practical geometry problems. This approach is similar to that for solving almost a word problem, but is geared slightly more toward the characteristics of geometry problems in particular.
1. Determine what you need to calculate to solve the problem. In some cases, you may need a length; in others, an area or angle measure. If you are conscious throughout the process of what you need to determine, you can save yourself a significant amount of time.
2. Draw a diagram. Sometimes a straightedge, compass, protractor, or some combination of these tools can be helpful. Even if you only use a rough sketch, however, making a visual representation of the problem can help you organize your thoughts and keep track of important information such as the relationship of line segments and angles as well as the measures thereof.
3. Record all appropriate measurements. If you are calculating an area, for instance, you may need to take measurements of certain lengths (alternatively, these may be provided to you). In either case, record them and mark them in some manner on your diagram.
4. Pay attention to units. Using units of square meters for a length or angle measure can be an embarrassing mistake! Keep careful track of the units you are using throughout the problem. If no units are given, simply use the generic term "units" in place of inches or meters, for example.
5. Divide the figure, if necessary, into manageable portions. If your diagram is a composite figure, it may help to divide the figure into bite-sized portions that you can handle.
6. Identify any appropriate geometric relationships. This step can greatly simplify the problem. Perhaps you can show two triangles to be congruent or similar, or perhaps you can identify congruent segments or angles. Use this step to fill in as much missing information in your diagram as you can.
7. Do the math. At this point, you need to apply what you've learned to analyze the figure and other data to solve the problem. You may, for example, need to apply the Pythagorean theorem, or you may need to calculate the perimeter of a figure. Whatever the details of the problem, you will need to apply your skills in geometry in an appropriate manner.
8. Check your results. Take a look at your answer in the context of your diagram-does your answer make sense? A result of millions of square meters for the area of a figure with dimensions in the range of a few meters should tell you that you've made an error at some point in your analysis.
Not every step of the approach outlined above will be needed in every problem. You must use your best judgment in determining what is necessary to solve the problem in a satisfactory and time-efficient manner. Also, you may not always think to use the exact progression of steps above; the outline is simply a way to describe a systematic approach to problem solving. The remainder of this article provides you the opportunity to test your geometry skills by way of several practice problems. Obviously, these problems do not require you to go out and make any measurements of lengths or angles, but keep in mind that problems you encounter in everyday life may require you to do so!
Practice Problem: The floor plan of a house is shown below. Determine the area covered by the house.
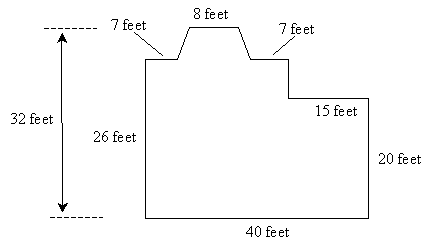

Solution: Let's first divide the diagram of the house into two rectangles and a trapezoid, since we can calculate the area of each of these figures. Using the properties of each figure, we can also fill in some of the unknown information.
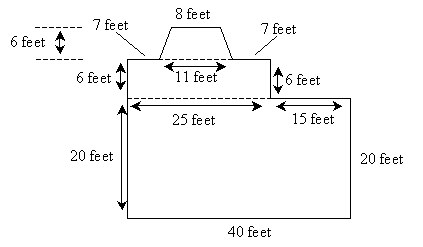
Now, the area of the larger rectangle is the product of 40 feet and 20 feet, or 800 square feet. The area of the smaller rectangle is 25 feet times 6 feet, or 150 square feet. The area of the trapezoid is the following:
![]()
The height (h) is 6 feet, and the two bases (b1 and b2) are 8 and 11 feet.
![]()
Adding all three areas gives us a total area of the house of 1,007 square feet.
Practice Problem: A hiker is walking up a steep hill. The slope of the hill between two trees is constant, and the base of one tree is 100 meters higher than the other. If the horizontal distance between the trees is 400 meters, how far must the hiker walk to get from one tree to the next?
Solution: Because this problem may be difficult to envision, a diagram is extremely helpful. Notice that the base of the trees differ in height by 100 meters--this is our vertical distance for the walk. The horizontal distance is 400 meters.
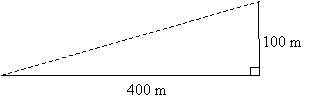
Note that we have shown the right angle because horizontal and vertical segments are perpendicular. We can now use the Pythagorean theorem to calculate the distance d the hiker must walk.
![]()
![]()
Thus, the hiker must walk about 412 meters. Note that although the hiker makes a significant (100 meter) change in elevation over this walk, the difference between the actual distance he walks and the horizontal distance is small--only about 12 meters.
Practice Problem: A homeowner has a rectangular fenced-in yard, and he wants to put mulch on his triangular gardens, as shown below. The inside border of each garden always meets the fence at the same angle. If a bag of mulch covers about 50 square feet, how many bags of mulch should the homeowner buy to cover his gardens?
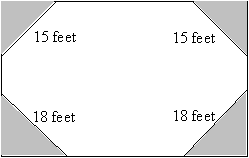
Solution: We are told in the problem that the inside border of each garden meets the fence at the same angle in every case; thus, we can conclude (as shown below) that the triangles are all isosceles (and that the triangles with the same side lengths are congruent by the ASA condition). We can thus mark each side with an unknown variable x or y.
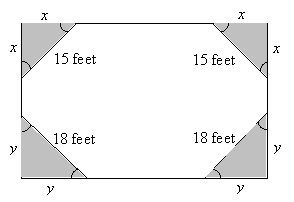

Recall that the fenced-in area is rectangular; thus the angle in each corner is 90°. We can then solve for x and y using the Pythagorean theorem. Notice first, however, that x and y are the height and base of their respective triangles.
![]()
![]()
![]()
![]()
Because the gardens include two of each triangle shape, the total garden area is simply the sum of x2 and y2. (If you do not follow this point, simply use the triangle area formula in each case--you will get the same result.)
![]()
Thus, the homeowner needs six bags of mulch (for a total of 300 square feet) to cover his gardens. (Of course, we are assuming here that he must buy a whole number of bags.)
























