Key Terms
o Sinusoidal waves
o Periodic
o Amplitude
o Frequency
o Angular frequency
o Phase
o Frequency spectrum
Objectives
o Recognize that an arbitrary waveform can be broken into a set of sinusoidal waves
o Learn how to calculate the parameters (such as frequency and amplitude) of sine waves
o Recognize some simple manifestations of frequency spectra, such as in graphic equalizers and prisms
Let's Begin!
This article provides us with some mathematical tools for studying acoustic waves (also known as sound waves, a type of mechanical wave) and electromagnetic waves (also known as light waves).
Wave Basics
You're likely familiar with the effects that result from dropping a stone into a still pond or other body of water. A series of waves begin traveling outward in concentric circles that get larger with time. In fact, we can learn much about sound (and light) waves by considering this analogy (or any similar analogy involving water, whether it be steady swells on the ocean or waves at the beach). Before we consider sound waves specifically, however, we will review some basic principles of waves in general.
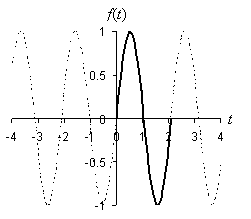
Consider some arbitrary waveform, such as that shown below. The horizontal axis might be time or displacement (distance), and the vertical axis might be pressure variation (in the case of sound waves) or electric field variation (in the case of light waves). For the sake of illustration, we'll label the horizontal axis as time and the vertical axis as the arbitrary function f(t).
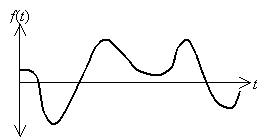
As it turns out, any arbitrary "waveform" f(t) can be constructed from (usually an infinite number of) sinusoidal waves, which are waves (or simply functions) of the form A sin (?t + ?). By adding these sinusoidal functions with appropriate values of ? and ?, an arbitrary function (such as f(t) above) can be obtained. Of course, this process is not simple; the details of this topic are beyond the scope of this article, but advanced students may wish to study the topic further. For our purposes, we need only know that any given waveform can be broken into a set of constituent sinusoidal functions that, when added, produce the waveform.
Let's first consider some of the characteristics of the function f(t) = A sin(?t + ?). A plot of this function for ? = 0 and A = 1 is shown below for ? = 1, ? = 2, and ? = 3.
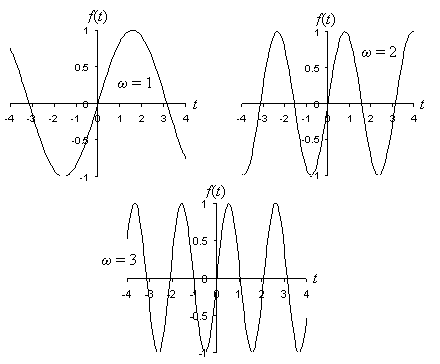
Notice first that the sine function is periodic--that is, it has a pattern that repeats at regular intervals (much like a wave in the water!). In each case, the function has a maximum of 1 and a minimum of –1; we call half the distance between the peak (the maximum value) and the trough (the minimum value) the amplitude of the sine function. The amplitude is simply equal to the coefficient A of the sine function; in this case, it is simply 1. Similarly, the amplitude of 5sin(?t + ?) is 5, for instance. The units of the amplitude A also determine the units of the function as a whole--thus, if A is 100 volts per meter, for instance, then the function f(t) has units of volts per meter.
Returning to the plots of the functions shown in the above diagram, we can see that ? governs the frequency (how often the function's fundamental pattern repeats) of the sine wave: a larger value of ? means more repetition in a given amount of time. (Actually, ? is the angular frequency--we will define the frequency in a moment.) Consider the case of ? = 3; a single fundamental unit of the function is shown in the plot below as a solid line (other fundamental units can be chosen--this one is easy to see, however). Perhaps a simpler fundamental unit is simply the portion of the sine wave between two successive peaks or two successive troughs; any of these or other similar choices is legitimate.
The sine function (specifically, sin(?t)) is zero for arguments that are multiples of ? (n? for any integer n). Let's calculate the period of the sine function, which is (in this case) the time between the beginning and end of the fundamental repeating unit of the function. In this case, the period is the difference in time between the first and third crossings of the horizontal axis. On the basis of the characteristics of the sine function, the first three crossings (or zeros) are sin 0 = 0, sin ? = 0, and sin 2? = 0. Thus, the fundamental repeating unit of the sine function starts at ?t = 0 (or t = 0) and ends at ?t = 2? (or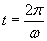 
). The period T of the sine function is then the following. If t is measured in seconds, then T also has units of seconds.
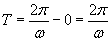
If the sine function has a fundamental repeating unit that is T seconds in length, then the function repeats once every T seconds. Thus, we define the frequency f as follows, where f has units of inverse seconds (also called hertz, or Hz).
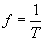
The term ? is actually what we call the angular frequency, and it is related to f by the expression ? = 2?f. Thus, we can also write the sine function as A sin(2?ft + ?).
We now need only determine what effect the term ? has on the function A sin(?t + ?). Let's plot several sine functions with ? = 1 and A = 1, but with ? set to 0, 1, and 2, respectively.
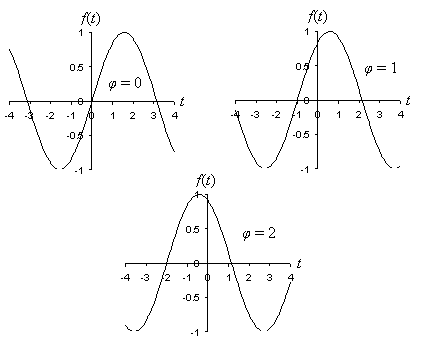
Notice that altering the value of ? has the effect of shifting the sine function to the left. The term ? is called the phase of the function. We will largely ignore the phase of the sine function for the sake of simplicity. Phase, however, is an important characteristic of a sine wave.
Practice Problem: Find the amplitude and frequency of the function f(t) = 1.5 sin(7t), where t is measured in seconds.
Solution: Let's plot this function to help us visualize the problem and to later check our answers.
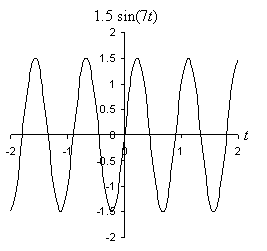
Recall that the amplitude of a sine function is the coefficient; in this case, the amplitude is simply 1.5. Concomitantly, we can see in the plot of the function that the maximum is 1.5 and the minimum is –1.5. To calculate the frequency, we can note that the function follows the pattern of A sin(?t), where ? = 7 in this case. Because we defined ? as 2?f, we can solve for f as follows.
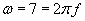
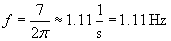
In other words, the fundamental unit of the sine function repeats slight more often than once per second; we can also see this in the plot of the function, since the "upward" crossing of the t-axis occurs at slightly less than one second.
Practice Problem: A scientist is using a pile supporting a long pier to take measurements of waves near a beach. Using a ruler on the pile, he finds that the waves have a maximum height measurement of 5 meters and a minimum height measurement of 3 meters on the pile. The scientist measures the time between successive wave peaks as 4 seconds. Write a function that describes this wave action mathematically.
Solution: Assuming these waves are sinusoidal, we need only calculate the amplitude and frequency of the waves to provide enough information for writing a function that describes them. This function f(t) has the following form:
f(t) = A sin(?t)
We leave out the phase because it does not have any fundamental effect on how we're describing the water waves. (If the scientist wanted to describe the waves starting from a specific wave height at t = 0, for instance, then the phase would be a necessary component of the mathematical description.) First, we can calculate the amplitude A of the waves by finding half the vertical distance between the peak and trough of the wave.
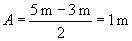
Second, we'll calculate the frequency of the waves. The scientist measures the distance between successive peaks as 4 seconds--thus, the wave pattern repeats every 4 seconds, and the frequency f is the following.
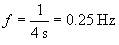
From this value, we can also calculate ?.
? = 2?f ? 1.57 Hz
The function f(t) describing the water waves is then the following, where t is measured in seconds.
f(t) = sin(1.57t) m
The Usefulness of Sine Functions
Because we are able to easily examine and understand the characteristics and behavior of sine functions, our ability to break down an arbitrary waveform into component sine functions is extremely helpful. For instance, we can characterize a waveform in terms of its frequency spectrum. Recall from above that we can break a waveform f(t) into a sum of functions of the form A sin(2?ft + ?), where A, f, and ? have different values for each component sine function. Each frequency, f, has an associated amplitude, A. Thus, in the case of sound waves, lower-pitch tones may be louder (that is, they may have higher amplitudes) than higher-pitch tones (or vice versa). If you've ever adjusted the graphic equalizer on a stereo (or if you've simply changed the bass or treble on your radio), then you've altered the amplitudes of the sinusoidal components of the music or other audio that you've been listening to! In the context of electromagnetic waves (light), a prism takes one waveform and breaks it into its component waveforms (or colors). The prism can "break" sunlight, for instance, into a rainbow of colors, ranging from lower-frequency red light to higher-frequency violet light. (Not coincidentally, the rainbow is also sometimes called a color spectrum.)
