Key Terms
o Units
o Unit conversion
Objectives
o Develop an organized approach to tackling word problems
o Learn how to handle units
o Practice solving word problems
Introduction to Word Problems
Before you start solving word problems in algebra, you should first already know about real numbers, how to manipulate algebraic expressions, and how to solve math problems involving linear equations and inequalities. We will focus on application of these concepts through word problems. First, we'll review a few basic steps that will help you solve word problems.
At this point, the mathematical aspects of word problems shouldn't pose much difficulty for you. The main difficulty is translation of the details of the word problem into the kinds of mathematical expressions that you have learned to handle. Here are some steps that will help you organize the process of translating from words to mathematical expressions that you can solve.
1. Read the problem. This step may seem obvious, but you will save yourself much time and difficulty if you first take some time to carefully read what the problem says. You may not be able to visualize all the details, but you should gain a mental picture of what is generally being discussed.
2. Determine what the problem is asking for. A word problem may provide you with enough details to calculate all sorts of parameters, but the problem probably will only be asking for one or two. Thus, figure out what you are trying to find and write it down.
3. Draw a diagram. You don't need to be an artist to do this-just draw something that you can understand and that helps you organize your thoughts about the problem. If the problem involves a moving automobile, for instance, you don't need to draw a professional rendition when a box or something similar (even marked "car" if necessary) will do.
4. Identify the variables (unknown parameters). The mathematical expressions that you glean from the word problem will involve an unknown value (or values) at some point (one of which may be the result from step 2 above); try to identify what this value is and assign it a variable symbol. Write down this assignment for reference as you solve the problem (for instance, "v = the velocity of the car").
5. Pay attention to units. Problems from the real world involve units, and you need to keep track of them.
6. Write mathematical expressions. This is the critical step: translation of the information that you get from the problem into math. If you have carefully performed the preceding steps, you should be in good shape to write the correct expressions.
7. Solve the math problem. Take the results of step 5 and use the algebra skills you've learned to solve the problem. The result should be a solution that fulfills the requirement you wrote down in step 2 (that is, whatever the problem is asking for).
8. Check your results. Look at your final answer and ask yourself if it makes sense. Does the problem ask for a speed but you've ended up with units of acceleration in your answer? You've probably gone astray somewhere along the line. Check to see if the number is reasonable (for example, your average automobile can't be expected to go 1,000,000 miles per hour!).
Unit Analysis
Before we look at a few example problems, we need to first consider the use of units and unit analysis. Units are simply identifiers that describe what a number is quantifying. For instance, we can talk about 1 banana, 1 meter, 1 liter, 1 mile per hour, 1 ton, or a limitless variety of other things. Units act in many ways like multiplicative constants: they multiply and divide like any other factor, and they can cancel each other out when they are the same. Let's look at a couple quick examples (note that although these examples use plural and singular units for ease of reading, whether a unit is written in its plural or singular form has no bearing on the meaning or the math):
![]()
![]()
This second example is actually a case of identity, because 12 inches = 1 foot. This is called unit conversion. We can thus see how the presence of units has an effect on the math, but the same general principles that we have studied still hold.
Practice Problem: How many minutes are in a year (assume 365 days)?
Solution: We can solve this problem in a lucid manner by using what we have learned about units. We are looking for an expression of the form 1 year = x minutes. Let's multiply by factors with corresponding units that convert from years to seconds as follows. (Again, note that we are actually multiplying in each case by 1 because of the relationship of the units.)
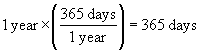
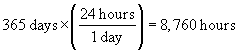
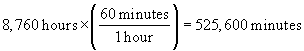
Thus, 1 year = 525,600 minutes, or (alternatively) there are 525,600 minutes in a year. This problem illustrates the process of unit conversion; a year is the same as 525,600 minutes even though 1 ≠ 525,600.
Example Word Problems
Now that we have briefly reviewed units and unit analysis, let's look at a couple sample word problems.
Practice Problem: Bill takes a trip in which he drives a third of the time at 30 miles per hour, a third of the time at 50 miles per hour, and a third of the time at 70 miles per hour. If his trip was 450 miles, how long did it take him to reach his destination?
Solution: As a first word problem, this one may seem a bit intimidating; don't let it discourage you, though. You may be surprised at how far you can get by approaching the problem systematically. First, let's identify what the problem is asking for: a total trip time, which we can call t.
t = total trip time
Let's now draw a diagram-it need not be to scale. Let's just get something down that we can refer to easily.
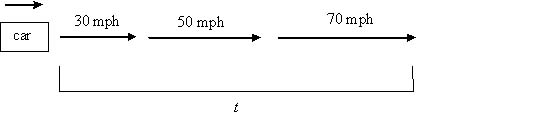
The variable (unknown) in the problem is t, which is the value we want to calculate. We know that we can find the distance traveled by multiplying the speed and the time traveled at that speed (for instance, if we travel 2 hours at 30 miles per hour, we have gone 60 miles). In addition, we know that Bill travels a third of the time (t/3) at each of the speeds mentioned, so we need to add the three trip segments to get the total distance of 450 miles. Let's write the algebraic expression:
![]()
We now want to solve for t. (If the units really trip you up, you can eliminate them if you are certain that the resulting units on each side of the equality will match exactly.)
![]()
![]()
![]()
Note carefully how we treat the units in this next step.
![]()
![]()
The total trip thus required 9 hours. Let's check the result: one-third of the total trip time is three hours. Thus,
![]()
![]()
The result thus checks out.
Practice Problem: The Celsius (C) and Fahrenheit (F) temperature scales are related by a linear function. If the boiling point of water is ![]() and the melting point of water is
and the melting point of water is ![]() , find the linear functions that convert from one scale to the other.
, find the linear functions that convert from one scale to the other.
Solution: This problem asks us to find a conversion function that takes a Fahrenheit temperature reading and turns it into a Celsius temperature reading. (The inverse function does just the opposite.) Let's call f the temperature reading in degrees Fahrenheit and let's call c(f) the conversion function from Fahrenheit to Celsius. The problem tells us that these two scales are related by a linear function; we thus know that we can write c(f) using the equation of a line with unknown variable f.
c(f) = mf + b
Here, m is the slope of this line and b is the y-intercept. Because we are given what amounts to two points on a graph that relates c to f, we can calculate the parameters m and b. The points, in (f, c(f)) form are the boiling point of water--(212 F, 100 C)--and the melting point of water--(32 F, 0 C). Let's substitute the melting point values into the equation and simplify.
![]()
We can note that for the units to match, b must have units of degrees C, and m must have units of degrees C per degree F (C/F). Let's then eliminate the units to simplify manipulations.
c(32) = 0 = 32m + b
b = –32m
Now, we can use this result along with the boiling point of water.
c(212) = 100 = 212m – 32m
100 = 180m
m = ![]()
Then
b = –32![]() =
= ![]()
The conversion function from Fahrenheit to Celsius is then c(f) = ![]() f –
f – ![]() (again, we have left off the units, but to be clear, c(f) is a value in degrees Celsius and f is a value in degrees Fahrenheit). We can test this result by substituting either or both of the known temperature values.
(again, we have left off the units, but to be clear, c(f) is a value in degrees Celsius and f is a value in degrees Fahrenheit). We can test this result by substituting either or both of the known temperature values.
c(212) = ![]() (212) –
(212) – ![]() = 100
= 100
To find the inverse function, which converts from Celsius to Fahrenheit, we simply solve for f, which we can then express as a function of c.
c = ![]() f(c) –
f(c) – ![]()
![]() f(c) = c +
f(c) = c + ![]()
f(c) = ![]() c + 32
c + 32
Let's test this result:
f(0) = ![]() (0) + 32 = 32
(0) + 32 = 32
























