Key Terms

 

o         Associative

o         Distributive

 

Objectives

 

o         Identify additional properties of multiplication and addition (associative and distributive properties)

o         Be able to add, subtract, multiply, and divide radical expressions

o         Simplify radical expressions when appropriate

 

 

Primer for Arithmetic Operations on Radicals

 

We will look carefully at how to work with radicals by way of arithmetic operations (addition, subtraction, division, and multiplication). First, we introduce a mathematical concept that may or may not be familiar to you, but that is crucial to properly understanding this topic. When we multiply two numbers, for instance, we can generally write the product as another number. For example, . But what if one of the factors is unknown or cannot be written in an exact form? Let's consider multiplication of 4 by some unknown number c.

 

 

We cannot simplify this expression further or write it as a single known number (because c is unknown). Likewise, consider multiplication of 4 by an irrational number . Because we cannot write as an exact decimal or as a fraction with integers in the numerator and denominator, we cannot write the product (in this case) as an exact decimal or a fraction.

 

 

Thus, the way we will treat radicals is very similar to the way we must treat unknown numbers. We will leave them (in many cases) in radical form, knowing that they correspond to a specific, known number, but in the interest of exactness, we will not attempt to evaluate the radical. The results of any arithmetic operations will, in such cases, be expressions that include radicals.

 

Some Additional Properties of Multiplication and Addition

 

Recall that we identified addition and multiplication as commutative operations. Thus, for any two numbers a and b,

 

 

To aid in our look at radical operations, we can also consider some additional properties of addition and multiplication (and, by implication, subtraction and division, since these operations can be rewritten as addition and multiplication, respectively). First, we note that addition and multiplication are both associative, meaning that we can group terms or factors in any way we wish. Given three numbers a, b, and c,

 

 

This property simply says that we can perform a series of additions or multiplications in any order. (Recall from our study of the order of operations that expressions in parentheses must be evaluated first-hence we express the associative property as we have above.)

 

Additionally, we can show that multiplication is distributive, meaning that if we multiply a number a by the sum b + c, then

 

 

We can illustrate this property in a more concrete manner by considering that the product of two factors x and y can be viewed as x sets of y objects. For instance, 7 sets of 8 objects is equal to 56 objects. But 7 sets of 8 is the same as 3 sets of 8 and 4 sets of 8, or 2 sets of 8 and 5 sets of 8. Consider a graphical illustration of multiplication for this example.

 

 

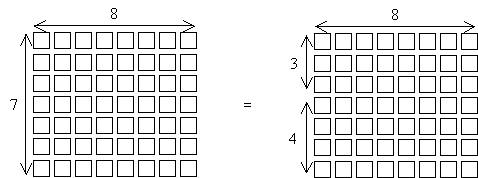
Note above that and that . Furthermore, according to the representation of multiplication that we have used above, not only is , but . Thus, we can see from this example that multiplication is indeed distributive.

 

 

We can now apply these concepts and properties to our understanding of radicals.

 

Radical Operations

 

Let's say we wanted to perform the following addition:

 

 

As we have discussed, the square root of a number that is not a perfect square is irrational; thus, we cannot express it exactly as either a finite decimal or a fraction containing an integer numerator and integer denominator. Note, however, that we can use the fact that multiplication is distributive: . We'll start by rewriting the radical expressions slightly-this does not change the value of the expression, however.

 

 

Note that we cannot simplify this expression any further and still keep it exact. Also, note that we can omit the multiplication symbol () whenever doing so does not affect the clarity of the expression. Thus, we will, for the most part, omit this symbol for the remainder of this article. Let's look at a couple other examples.

 

 

Note that we cannot perform these operations if the numbers under the radicals are different. Thus, for instance, the expressions below cannot be further simplified.

 

 

We can also multiply and divide radicals.

 

 

 

Practice Problem: Evaluate each expression, where possible.

 

e.     f.

 

Solution: In each case, simply follow the pattern demonstrated earlier. Until you get more familiar with the operations, you may need to very carefully follow the distributive property to find sums or differences of radical expressions. Note that the expression in part a cannot be evaluated any further; the expression in part f can be only partially evaluated.

 

 

 

 

 

Simplifying Radicals

 

To aid in performing the operations above, we must often simplify radicals. To illustrate, consider the following expression.

 

 

A cursory look at this expression might seem to indicate that the expression cannot be simplified any further. Nevertheless, if we simplify the radical in the second term, we will find that we can actually perform the addition. The manipulations below rely only on the rules we have discussed so far.

 

 

Thus,

 

 

Above, we simplified the radical expression ; this process is in some ways similar to reducing a fraction to lowest terms. In simplifying a radical, we are writing an equivalent expression that is easier to work with and that often leaves less room for error. The goal of this process is to write the radical expression such that the number under the radical is not divisible by a perfect square. For instance, in the radical expression , 8 is divisible by 4, which is a perfect square. As a result, we can simplify this expression by factoring out the 4, as we did above. We then calculate the square root of 4 (which is 2), leaving only a 2 under the radical. Since 2 is not divisible by any perfect squares, the radical form is in simplest form.

 

 

Practice Problem: Evaluate each radical expression, where possible.

 

 

 

f.

 

 

Another case where simplification is beneficial is a radical occurring in the denominator of a fraction. Consider the quotient expression we encountered above:

 

 

One (perfectly legitimate) approach to evaluating this expression is to take the square root of 16 (which is 4) and then simplify the radical in the denominator.

 

 

We are left, however, with a square root in the denominator. Although this is not an incorrect result, preventing occurrences of radicals in the denominator is often beneficial. Thus, we must find a way to remove the radical from the denominator. First, let's take note of the following, where y is any number:

 

 

Of course, multiplying any number by 1 yields the original number; furthermore, if the numerator and denominator of a fraction are the same, then that fraction is equal to 1. Thus, we can remove a radical from the denominator of a fraction by calculating an equivalent fraction in the manner shown below.

 

 

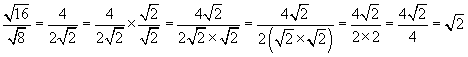
This is the same result we obtained earlier using a different approach to evaluating this expression. Below is another example of simplifying a fraction with a radical in the denominator.

 

 

Finally, note that in such cases, we can write the expression with the radical in the numerator or with the radical as a factor multiplied by a fraction.

 

 

 

Practice Problem: Simplify each of the following fractions.

 

a.      b.      c.       d.

 

Solution: In each case, multiply the numerator and denominator by the radical in the denominator and evaluate. Before doing so, however, performing other simplifications may make the process easier. In part c, the result can be written either as a single fraction or as a fraction minus an integer.

 

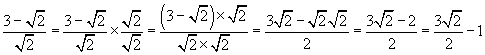
d.