?

Key Terms

o         Statistics

o         Average

o         (Arithmetic) mean

o         Median

Objectives

o         Calculate the average, mean, and median of a data set

o         Recognize that not all statistical values accurately describe a data set

Statistics is the field of study that focuses on collecting, interpreting, and representing sets of numerical data (that is, numbers). These numbers might consist of a set of scientific measurements, answers to survey questions, outcomes of some random event (such as the roll of a die), and so on. Because long lists of numbers can be tedious and difficult to work with and characterize, the field of statistics seeks to study data sets and reduce them to one or more numbers that accurately represent the qualities of the set as a whole. In any such endeavor, where a large set of data is reduced to a few descriptive terms or numbers, misrepresentation can be easy to do. Hence, a popular cultural sentiment is that statistical numbers are misleading. Although they need not necessarily be misleading, they can be if not calculated and represented with care and precision.

Finding the "Middle" of a Data Set

Let's say we wanted to describe a data set that consists of the ages of employees at a certain company. This data set might look something like the following, where each number represents the age of one and only one employee:

25, 27, 27, 30, 35, 37, 42, 45, 52, 63

Now, assume someone wanted us to describe the age of the employees in the company. Of course, we could simply read the above list, hoping that the interested party would stay interested through the entire list. Alternatively, we could attempt to describe the data set using some number in the "middle." The ages range between 25 and 63; we could simply find the age halfway between these numbers and call it the "middle." In this case, the result would be 44 years. The difficulty with this approach, however, is that this number is not necessarily representative of the data set if most of the employees are very near the high or low end of the range. For instance, if all but one or two employees were in their mid-20s, the age 44 would not accurately describe the ages of the employees.

 

Thus, the average age of employees at the company is 38.3. Note that this number is significantly different from the value of 44 that we calculated above. Also note that finding the value halfway between the maximum and minimum age is the same as calculating the average of the ages of the youngest and oldest employees. This result, however, does not take into account how the employees in between are distributed (whether they are generally on the older or younger end of the range).

Practice Problem: A scientist is taking a series of measurements and gets the following results. Calculate the average of his measurements.

1.2, 1.3, 1.3, 1.3, 1.4, 1.6, 1.7

Solution: To calculate the average, μ, add all the values in the set and divide the sum by 7 (the total number of values in the set).

Thus, the average measurement is 1.4.

Let's consider a data set that is obviously skewed toward the higher end of its range. The following data might be the outcome of a series of rolls of a loaded (unfair) 10-sided die (with sides labeled 1 through 10). The results are ordered from smallest to largest for the purpose of illustration. The data set contains the outcomes of 12 rolls of the die.

1, 2, 4, 6, 7, 8, 8, 9, 9, 10, 10, 10

Let's calculate the average μ:

But only a few values are less than the average (1, 2, 4, and 6), whereas most of the values are more than the average (8, 8, 9, 9, 10, 10, and 10). In cases such as these the average may not be the best way to describe the data set. Another measure of the "middle" of the set is the median. The median M of a data set is the value for which half of the values in the data set are greater than M and half are less than M. (In some cases, the median is the value for which half the values are less than or equal to M and/or half the values are greater than or equal to M.) Thus, if a data set contains five values ordered from lowest to highest, the median is the third value. For instance, the median of the data set {1, 3, 4, 7, 10} is 4. If the data set contains an even number of values, the median is the average (mean) of the two central values. For instance, the median of the set {1, 3, 4, 6, 7, 10} is the average of 4 and 6-in this case, 5.

Looking once more at the data from the rolled die, note that it contains 12 values (an even number). We can thus calculate the median M by averaging the two center values (underscored below).

1, 2, 4, 6, 7, 8, 8, 9, 9, 10, 10, 10

The average of 8 and 8 is, of course, 8. Thus, the median of this data set is 8, a value that is higher and that better indicates the "center" of the data set, since most of the numbers are greater than 7 (the average of the data set).

Practice Problem: Calculate the median of the data set below.

1, 5, 9, 2, 4, 7, 2, 4, 6, 3

Solution: First, we need to order the data set from least to greatest.

1, 2, 2, 3, 4, 4, 5, 6, 7, 9

The median M of the data set is the middle value (such that half the values are greater than or equal to M and half are less than or equal to M). In this case, because we have an even number of values, we must average the middle two values--4 and 4. The average (and thus the median) is

The median is 4.

A third way to characterize a data set is the mode, which is the value that occurs most frequently. The mode does not always indicate the "middle" of a data set, but it can be a good indicator of which value is most common. Assume a series of rolls of a six-sided die turned up the following results (not necessarily in order):

1, 3, 2, 3, 4, 3, 6, 5, 3, 5, 3, 3, 2, 3, 6, 3, 3, 6, 1, 3

Of the numbers rolled (20 total), half of them were the number 3. Someone who is planning to bet on the next roll would likely not be interested in the average (mean) roll or in the median roll. Rather, he would probably want to know the mode: the number that comes up most often. In this case, the mode is 3, and our gambler might be inclined to place his money on this number.

Practice Problem: Find the mode of the data below.

1, 1, 1, 3, 4, 5, 5, 5, 5, 6, 7, 8, 8, 8

Solution: The mode is the value that occurs most frequently. Note that the number 5 occurs four times--more than any other number in the set. Thus, the mode is 5.

Being Careful with Statistics

Although we have not looked at some of the other ways of describing a data set (such as how widely the data is spread about the mean, or how it is skewed to either side of the mean), we have shown that describing a data set using one or two numbers is possible. Nevertheless, as indicated from the start, reducing a large data set to just a number or two can produce misleading information. For instance, consider a set of data describing the incomes of citizens in a certain region. Assume that the (small) data set below, which lists individual income in increments of $10,000, is representative of the region:

10, 12, 13, 15, 18, 20, 20, 22, 23, 150

The average income is the following:

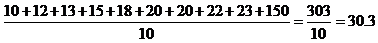
An ignoble politician might use this data to say that his constituents make an average of about $30,000 per year. This is true, as we calculated above, but it can be misleading, since virtually the entire population makes much less than $30,000. (A single uncharacteristic value can drastically alter the average of a data set.) In this case, the data set is best described using the median income, which is $19,000 (calculate the average of the middle values, 18 and 20). Thus, statistics can be helpful, but they must be used and interpreted with great care!