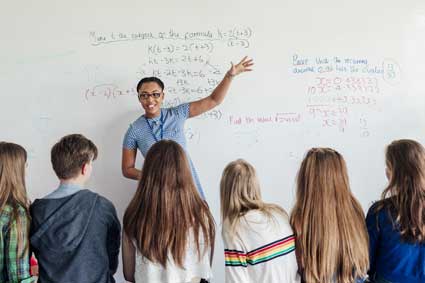Key Terms
o Polyhedron
o Face
o Edge
o Prism
o Right prism
Objectives
o Recognize polyhedra and prisms and be able to analyze simple examples of these figures
o Know how to use the formulas for volume and surface area for spheres and cylinders
First, we will consider the volume and surface area of some simple three-dimensional figures, then we turn to composite figures in three dimensions.
Volume and Surface Area
We will consider two basic types of geometric solids: polyhedra and spheres. A polyhedron is essentially an n-sided solid figure--it is the three-dimensional analog of a polygon. Some examples of polyhedra are shown below.

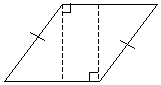
Polyhedra are defined by their faces, which are polygon regions, edges, which are the line segments that outline the faces and therefore the polyhedron, and vertices, which are defined in the same manner as they are for polygons. A specific type of polyhedron is a prism, which is a polyhedron with an identical (and parallel) top and bottom. If the sides of the prism meet the top and bottom at right angles, then it is called a right prism. The two polyhedra on the left side of the row of examples above are prisms--we can see this more accurately by using dashed lines to show the portions that are out of sight.
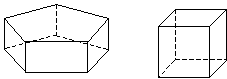
Again, notice that the top and bottom faces (bases) are identical; furthermore, these are actually right prisms (assuming the angles formed between sides and bases are right, as they appear to be in the diagrams). Clearly, the volume V of a right prism is simply the area A of the base times the height h of the sides, as shown for the cube (a six-sided prism) below.

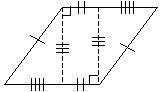
But what if the prism is not a right prism? The same formula applies. Let's take a look at why this is the case, once again using the six-sided prism. We'll look at this figure "on end" such that its depth is perpendicular to the surface of the page (in other words, the two bases are not visible). We know from the definition of a prism that opposite line segments (edges) are congruent.
Now, let's divide the solid as shown below, forming two triangular solids and one rectangular solid. Note that the dashed line is also the height of the prism.
From the properties of rectangles, we know the following.
By the SSS condition, we therefore know that the two triangles are congruent. Let's label the figure as follows, noting that the base b of the figure is equal to b1 + b2.
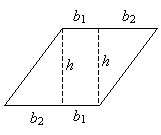
We can now calculate the area of this face of the figure.
![]()
But the area of bases is unchanged between the right and non-right versions of the prism. In other words, the depth in this case and in the case of the right prism (if oriented in the same way) is the same. Consequently, the volume is also the same. Although we have only demonstrated this fact for six-sided prisms, the same applies to all prisms: the volume is the area of the base multiplied by the height.
Practice Problem: Calculate the volume of the prism shown below.
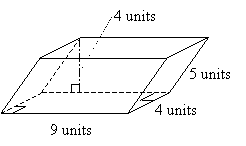

Solution: The polyhedron in the diagram is identified as a prism. On the basis of the right angles in the base (and thus both bases), we can identify the bases as rectangles with lengths of 4 units and widths of 9 units. Thus, the area of the base of the prism is 36 square units. The height of the prism is shown in the diagram as 4 units. Thus, we can calculate the volume V of the prism as follows.
V = bh = (36 units2)(4 units) = 144 units3
The volume of general polyhedra can be difficult to calculate, so we will not consider these in any greater depth. Formulas are available in books and on the Internet, however, for certain polyhedra.
Another parameter that we can calculate is the surface area of the figure. Regardless of the polyhedron, the surface area is simply the sum of the areas of all the faces of the figure. In the case of a cube (a six-sided prism), for instance, the surface area is simply six times the area of any face (the faces all have the same area, since all edges are congruent). (Or, if each edge has a length s, the surface area is 6s2.)
Practice Problem: Calculate the surface area of the prism from the preceding practice problem, assuming that the figure is only slanted to the right.
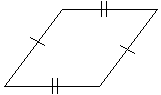
Solution: Look once again at the prism diagram in the first practice problem. We can find the surface area by calculating the area of each face. We already know that the bases each have an area of 36 square units. That leaves the four unknown sides. The problem tells us that the figure is only slanted to the right (shown in the diagram below with an arc)--thus, the only non-right angles are in the front and back faces. These two faces are parallelograms. The left and right faces are rectangles.
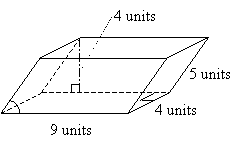

The left and right faces both have an area that is the product of 4 units and 5 units, or 20 square units. The front and back faces are parallelograms with bases of 9 units and heights of 4 units-each, therefore, has an area of 36 square units. Let's now find the total surface area, S.
S = (36 + 36) + (20 + 20) + (36 + 36) = 184 units3
Spheres are another type of three-dimensional figure whose volume and surface area can be calculated with relative ease. A sphere is the three-dimensional analog of a circle-it is defined by a center point O and a radius r. The sphere is the set of all points that are a distance r from O. An example of a sphere is shown below.


As with circles, it is difficult to derive formulas geometrically, but the formulas are well known. The volume V and surface area S are given below for a sphere of radius r.
![]()
![]()
A similar figure is the (circular) cylinder, which has two congruent circular bases and a tube-shaped body, as shown below. A cylinder is defined by the radius r of its bases and its height h.
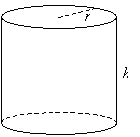

Similarly to a prism, the volume V of a cylinder is the product of the area of its base and the height.
V = πr2h
The surface area is slightly more complicated, but it can be calculated by simply extending our current knowledge. We know that the circumference of the base is 2πr; thus, if we simply multiply this formula by h, we have the surface area of the "barrel" of the cylinder. Now, we need only add the area of the bases, which is twice the area of either circular base. The total surface area S is then the following.
S = 2πrh + πr2 + πr2 = 2(πrh + πr2)
Practice Problem: A cylinder of height 16 feet and radius 5 feet is capped at each end by a hemisphere (half of a sphere), as shown below. What is the surface area and volume of the figure?
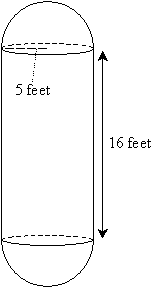
Solution: We already know how to calculate the surface area of the side of the cylinder: 2πrh. We must also calculate the surface area of the two hemispherical caps. Note that the "base" of the hemispheres is a cross section of the full sphere. Since this cross section has a radius of 5 feet, the hemispheres both have the same radius. The surface area of both hemispheres together is then simply the surface area of a full sphere of radius 5 feet. This surface area is 4πr2. We can now calculate the surface area of the figure.
S = 2π(5)(16) + 4π(5)2 = 160π + 100π = 260π ≈ 816.8 feet2
To calculate the volume, simply find the volume of the cylinder plus the volume of a sphere of radius 5 feet.
![]()
Composite Figures in Three Dimensions
Dealing with composite figures in three dimensions requires almost identical principles as those needed for dealing with composite figures in two dimensions. For instance, calculating the volume of a rectangular solid with a spherical empty space simply involves subtracting the volume of the sphere from the total volume inside the rectangular region. Also, our approach of dividing complicated figures into simpler and more easy-to-manage figures applies to three-dimensional figures as well. The following practice problem illustrates the approach for a three-dimensional figure.
Practice Problem: A rectangular prism contains two identical spherical cavities of radius 2 units, as shown below. Calculate the volume of the figure.
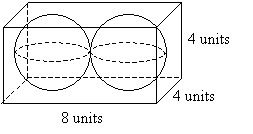
Solution: First, let's calculate the total volume within the rectangular prism. The base is 32 square units, and the height is 4 units. Thus, the volume is 128 cubic units. Each sphere has a radius of 2 units; thus, each has the following volume V.
![]()