Our number system is a base ten system which means it is based on ten numerals: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The eleventh numeral is a two-digit number starting with one for one ten plus nothing, 10, and the twenty-first numeral is a two digit number starting with two for two tens, 20. When we get to ten tens, we have a three digit number 100. This should sound a lot like the discussion earlier on place value.

 

Notice that a number that is less than one and has no integers with it usually has a zero in the integer's place to the left of the decimal point.

Any number that is not a mixed numeral can easily be divided or multiplied by 10 simply by moving the decimal point in the number.

All numbers have a decimal point – even if you don't see it! If it is a whole number or integer such as 6, the decimal point falls after the number such as 6. If it is exactly 6, it can be written as 6.0. If you needed to multiply it by 10, you would move the decimal point to the right one place because 10 has one zero on it. So 10 x 6.0 would be 60.

If you needed to multiply it by 10,000, you would move the decimal four places to the right because 10,000 has four zeros denoting that it is 10 x 10 x 10 x 10, so you would multiply 6 by 10 x 10 x 10 x 10, making it 60,000.

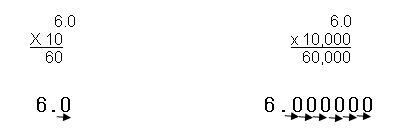
To divide by ten or a multiple of ten, you move the decimal point to the left by the same number of places as the number of zeros or decimal places in the number you are dividing by.

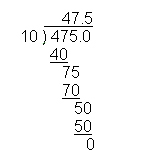
However, what you will soon realize after doing several such problems is that you have simply moved the decimal point to the left by one place when you divide by ten. You will also notice that if you divide by 1,000, you will move the decimal point three places to the left. Thus, 67,823 divided by 1,000 becomes 67.823.

 

Want to learn more? Take an online course in Basic Math.

 

If a number already has a decimal point in it, start with that decimal point and move it right if multiplying and left if dividing.

 

Converting Fractions to Decimals and Decimals to Fractions

 

In this case, the decimal came out even at the thousandths place. For this course, the fractions will come out as even decimals or you will be told how many places to express. You will have to work out the decimal one place beyond that in order to round off properly.

In the example above, you could have been told to round to the nearest hundredth. In that case, you would have worked the problem to the thousandths place where you have a 5. Since it is a 5 or larger, you would round the hundredths up one place and expressed the answer as 0.13. If you had been asked to express the answer to the nearest tenth, you would have worked it to the hundredths place. Then because the hundredths is a 2 (less than 5), you would have left it as a 2 – even though you know the next place will be a 5 or larger. Rounded to the nearest tenth: 0.1.

 

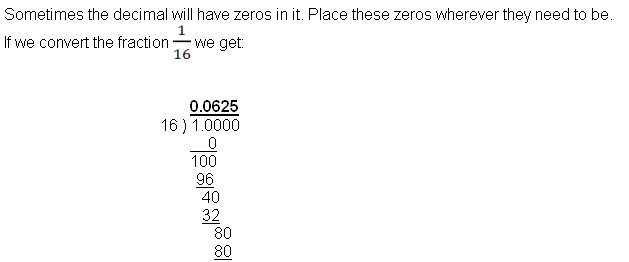
The zero is a placeholder to the right of the decimal point. If we did not use a zero as a placeholder, the number would be 0.625 which would indicate that 16 went into 10 six times! Instead it went into 100 six times. Therefore, be careful that you always use a zero as a placeholder if the divisor does not go into the dividend and you have to bring down another digit. 

Adding and subtracting decimals

Adding and subtracting decimals is not too different from adding and subtracting any numbers. It is critical that you write your decimals so that the decimal points align, or you will find yourself adding tenths to ones or subtracting hundredths from tenths.

As long as each of the numbers you are adding or subtracting has the same number of decimal places, the addition or subtraction is fairly easy.

 

In the first problem, you will need to put the decimal point after the five and then put the zero placeholders in the tenths and hundredths places. Obviously, you will then need to borrow one whole from the five to give you 10 tenths and then borrow one of the tenths to have 10 hundredths before you can subtract the 5 hundredths or 2 tenths.

 

 

Multiplying and dividing decimals

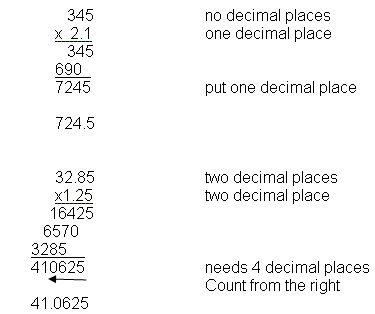
When you multiply decimals, do not align the decimal points. Simply line up the numbers along the right hand side of the problem. Then multiply just as you would if the numbers were all whole numbers and add at the end. After that count how many decimal places the two factors have (start at the far right of each number) and then give the answer that total number of decimal places.

 

 

To divide decimals, always use long division. If the divisor has a decimal, you will need to move the decimal point in the divisor and the dividend by the number of decimal places in the divisor so that the divisor becomes a whole number. You may need to add zeros as placeholders in the dividend. Then place a decimal point for the quotient directly above the final decimal point in the dividend and be careful to line up all the digits in the correct place values as you divide.