o Domain
o Range
o Relation
o Vertical line test
o One-to-one
o Horizontal line test
o Equation
o Solution
o Zero (of a function)
Objectives
o Learn more about functions (in general) and their properties
o Use graphs to explore a function's characteristics
o Gain an understanding of inverse functions and compositions of functions
o Understand the relationship between functions and equations
Properties of Functions
Recall that a function is a relation between certain sets of numbers, variables, or both. Let's now refine our understanding of a function and examine some of its properties. Fundamentally, a function takes an input value, performs some (perhaps very simple) conversion process, then yields an output value. Consider the function f(x) below:
![]()
The function f simply takes in input value x, multiplies it by 2, and then adds 3 to the result. We can therefore consider what constitutes the set of numbers that the function can accept as an input and what constitutes the set of numbers that the function can yield as an output.
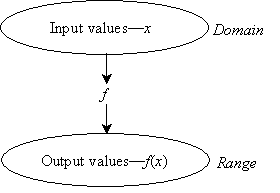

These sets are what we respectively call the domain and range of the function. The domain of a function is the set of numbers for which the function is defined. For instance, we may define a function G(n) over only the integers; thus, the variable n is only allowed to take on integer values when used in the function G. In some instances, the form of the function may exclude certain values from the domain because the output of the function would be undefined. Consider the example function h(y) below:
![]()
Notice that any value of y from the set of real numbers is acceptable-except for the number 4.
![]()
The result in this case is not defined; we thus exclude the number 4 from the domain of h. The range of h is therefore all ![]() (the symbol
(the symbol ![]() simply means "is an element of") where y ≠ 4.
simply means "is an element of") where y ≠ 4.
Practice Problem: Find the domain of the function ![]() .
.
Solution: The function g(x) simply takes the value x and turns it into its reciprocal value ![]() . Thus, for instance, the number 5 becomes
. Thus, for instance, the number 5 becomes ![]() , and
, and ![]() becomes 2. Note that any value of x works in this function as long as
becomes 2. Note that any value of x works in this function as long as ![]() is defined. As mentioned, fractions work as well as whole numbers, both for positive and negative values; the only value that does not work is 0, since
is defined. As mentioned, fractions work as well as whole numbers, both for positive and negative values; the only value that does not work is 0, since ![]() is undefined (how many times can 0 go into 1?). Thus, the domain of the function is all x in
is undefined (how many times can 0 go into 1?). Thus, the domain of the function is all x in ![]() where x ≠ 0. Let's look at the graph of the function also.
where x ≠ 0. Let's look at the graph of the function also.
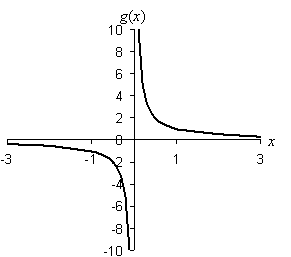

As you can see in the graph, the function g to the left of zero goes down toward negative infinity, but the right side goes toward positive infinity, and there is no crossing of the function at zero. Thus, we can see graphically that this function has a domain of all real values except 0.
The range of a function is the set of all possible values in the output of a function given the domain. In our example function h(y) above, the range is ![]() (except for h(y) = 0), because for any real number, we can find some value of y such that the real number is equal to h(y). Let's choose, for instance, –100. If we let y = 4.03, then
(except for h(y) = 0), because for any real number, we can find some value of y such that the real number is equal to h(y). Let's choose, for instance, –100. If we let y = 4.03, then
![]()
The same argument applies to other real numbers. In the case of h(y) = 0, however, there is no value of y large enough to make the fraction equal to zero. Thus, the range of h is all real numbers except 0.
At this point, we can make an important distinction between a function and the more general category of relations. For a relation to be a function specifically, every number in the domain must correspond to one and only one number in the range. Thus, if f(x) can have more than one value for some value x in the domain, then f is a relation but not a function. If f(x) has exactly one value for every x in the domain, then f is a function. Although it is often easy enough to determine if a relation is a function by looking at the algebraic expression, it is sometimes easier to use a graph. To do so, apply the vertical line test: look at the graph of the relation-as long as the relation does not cross any vertical line more than once, then the relation is a function.
Practice Problem: Determine if the relation ![]() is a function.
is a function.
Solution: We can easily note that for any value of y in the domain, the relation yields two different values in the range. For instance, if y = 4, h(y) can be either 2 or –2. The relation h(y) is therefore not a function. Let's look at the graph and apply the vertical line test as a double check:
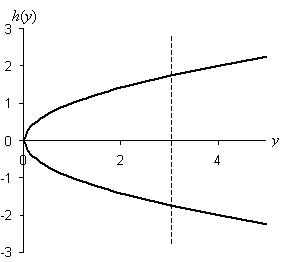

Note that the relation crosses a vertical line in two places almost everywhere (except at y = 0). Thus, the graph also proves that h(y) is not a function.
Also, it is helpful to make note of a special class of functions: those that are one-to-one. A function is one-to-one if it has exactly one value in the domain for each particular value in the range. (This property will be important when we discuss function inversion.) The example diagram below helps illustrate the differences between relations, functions, and one-to-one functions.
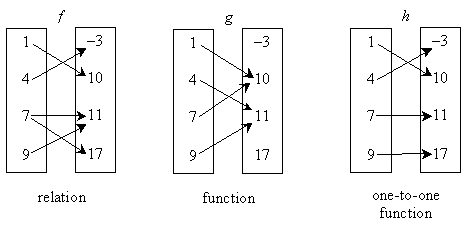

In each case, the diagram shows the domain on the left and the range on the right. The relation f is not a function because the f(7) = 11 and f(7) = 17 (that is, there is more than one value in the range for the value 7 in the domain). The relation g is a function because each value in the domain corresponds to only one value in the range. Finally, the relation h is a one-to-one function because each value in the domain corresponds to only one value in the range and vice versa. We can determine if a function is one-to-one by applying the horizontal line test. This test is similar to the vertical line test, except that it ensures that each value in the range corresponds to only one value in the domain. If, for every horizontal line, the function only crosses that line once, then the function is one-to-one.
Practice Problem: Find the range of ![]() .
.
Solution: A function such as this one is defined for all x values because there is no value of x for which 3x becomes infinity, for instance. Thus, the range of f(x) is ![]() , the entire set of real numbers. Another way to consider such problems is by way of a graph, as shown below.
, the entire set of real numbers. Another way to consider such problems is by way of a graph, as shown below.
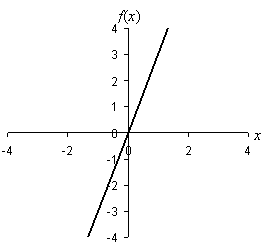

Note that the function is a straight line, and regardless of the scale of the axes (how far out you plot in any direction), the line continues unbroken. Thus, not only is ![]() the range of the function, it is also the domain. We can further observe that the function is one-to-one; you can see this by noting that the function simply takes every number on the number line and multiplies it by 3.
the range of the function, it is also the domain. We can further observe that the function is one-to-one; you can see this by noting that the function simply takes every number on the number line and multiplies it by 3.
Practice Problem: Determine if the relation ![]() is one-to-one.
is one-to-one.
Solution: First, we know that f(x) is a function because no value of x can cause f(x) to take on more than one value. Second, we can see that f(x) is not one-to-one because f(x) is the same for both +x and -x, since ![]() . Let's use a graph again to show this result visually.
. Let's use a graph again to show this result visually.
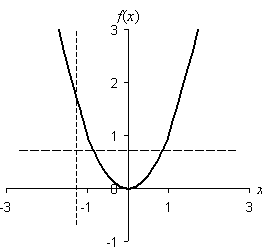

The graph above shows that the relation f(x) passes the vertical line test, but not the horizontal line test. Thus, f(x) is a function that is not one-to-one.
Inverses and Compositions of Functions
Two important manipulations of functions are compositions and inverses. A composition of functions is simply the replacement of the variable in one function by a different function. Thus, if we have two functions f(x) and g(y), the composition f(g(y)) (which is also written ![]() is found by simply replacing all instances of x in f(x) with the expression defined for the function g(y).
is found by simply replacing all instances of x in f(x) with the expression defined for the function g(y).
Practice Problem: Find the composition ![]() , where
, where ![]() and
and ![]() .
.
Solution: The composition ![]() is the same as h(r(s)); thus, we can solve this problem by substituting r(s) in place of s in the function h.
is the same as h(r(s)); thus, we can solve this problem by substituting r(s) in place of s in the function h.
![]()
Be careful to note that ![]() is not the same as
is not the same as ![]() :
:
![]()
An inverse of a one-to-one function f(x), which we write as ![]() , is a function where the composition
, is a function where the composition ![]() . An inverse of a function is, in this context, similar to the inverse of a number (3 and
. An inverse of a function is, in this context, similar to the inverse of a number (3 and ![]() , for instance). The inverse of a function can be found by making a switch: replace all instances of f(x) with x, and replace all instances of x with
, for instance). The inverse of a function can be found by making a switch: replace all instances of f(x) with x, and replace all instances of x with ![]() . Next, manipulate the equation using the rules of arithmetic and real numbers to find an expression for
. Next, manipulate the equation using the rules of arithmetic and real numbers to find an expression for ![]() . This is then the inverse of the function. Note that a function must be one-to-one to have an inverse.
. This is then the inverse of the function. Note that a function must be one-to-one to have an inverse.
Practice Problem: Find the inverse of the function ![]() .
.
We want to find the inverse of g(y), which is ![]() . Perform the replacement of g(y) with y, and y with
. Perform the replacement of g(y) with y, and y with ![]() .
.
![]()
![]()
Note that ![]() essentially acts like a variable, and it can be manipulated as such. So, let's rearrange this expression to find
essentially acts like a variable, and it can be manipulated as such. So, let's rearrange this expression to find ![]() . As with any arithmetic manipulation, as long as you perform the same operation on both sides of the equality sign (=), the equality will still hold.
. As with any arithmetic manipulation, as long as you perform the same operation on both sides of the equality sign (=), the equality will still hold.
![]()
![]()
![]()
Now, we can check the result using the condition of inverse functions:
![]()
![]()
![]()
The result checks out.
Equations
An equation in algebra is simply a statement that two relations are the same. Thus, an equation might be as simple as 0 = 0, or it might be as complicated as ![]() . A solution to an equation is the value (or values) of the variable (or variables) in an equation that makes the equation true. Finding a solution to an equation involves using the properties of real numbers as they apply to variables to manipulate the equation.
. A solution to an equation is the value (or values) of the variable (or variables) in an equation that makes the equation true. Finding a solution to an equation involves using the properties of real numbers as they apply to variables to manipulate the equation.
Closely related to the solution of an equation is the zero (or zeros) of a function. A zero of a function f(x) is the solution of the equation f(x) = 0. A function has a zero anywhere the function crosses the horizontal axis in its corresponding graph.

























