Kinetic energy is the energy of motion. An expression for kinetic energy is derived by looking at the case of an object that is lifted to some relative height (thus, work is done on this object) and then allowed to fall.
Key Terms
o Kinetic energy
Objectives
o Derive an expression for kinetic energy from the physics concept of work
o Understand the relationship of work and kinetic energy
o Calculate the kinetic energy of various objects
Let's Begin!
Relating Work and Kinetic Energy
In some sense, work is the amount of energy put into a task (or, perhaps, "put into the object"). For instance, imagine that we pick up some object off the floor and raise it to a certain height; we have done a certain amount of work on that object. If we let it go, however, it accelerates, as though that work we did in lifting the object is being turned into motion. Through this example, we can derive a definition for kinetic energy, which is energy of motion. This definition, as we will see, is closely related to how we have defined work.
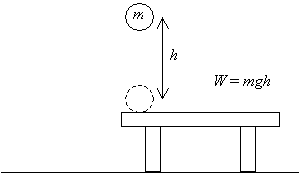
First, let's consider an object: a ball of mass m. We'll pick the ball up off a table and raise it a distance h above that table, as shown below. We have therefore done an amount of work W = mgh, (this result is the product of the magnitude of the displacement vector (h) and the applied force (mg)--the corresponding vectors are parallel).
Now, if we release that ball and let it fall from the height h above the table, once it returns to its original height (the level of the table), it will have a certain velocity v resulting from the acceleration due to gravity.
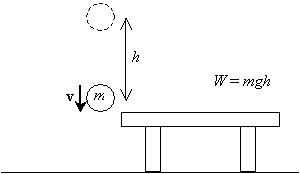
We want to calculate this velocity (or speed, technically--we may occasionally substitute the term velocity for speed, but always be aware that velocity is actually a vector and speed is the magnitude of the velocity). We know that the acceleration due to gravity is constant and that the initial velocity of the ball is zero (it is stationary before it is released). We will assume that the initial height of the ball is h and that its final height is zero (the level of the table). To calculate the velocity by deriving the appropriate formulas, we require the use of elementary integral calculus. (If you are an advanced student or are looking for an extra challenge, you can try deriving these formulas under the above conditions yourself. Simply note that the velocity v of the ball is the time rate of change of its position x as a function of time t,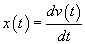 
, and that the acceleration a is the time rate of change of the velocity, 
.)
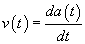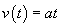
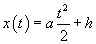
These formulas express the velocity as a function of time, v(t), and the position (height) as a function of time, x(t), in terms of the acceleration a, height h, and time t. We know that a = –g, since the ball is only accelerated by gravity and this acceleration is downward (hence the negative sign). The final position of the ball is zero meters, or x(t) = 0. Let's calculate t, the amount of time between the ball's release and its arrival at the level of the table.
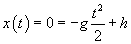
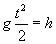
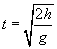
Now, let's calculate the velocity of the ball at this time.
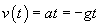
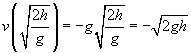
Let's now compare this result with the work originally done on the object: W = mgh. Note how close in form these two expressions are; in fact, the only factor missing from the velocity is the mass of the ball, m. If we squared the velocity, multiplied by m, and then divided by 2, we would in fact have the same expression as the work!
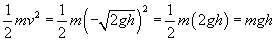
Thus, we can see in some sense how the definition of kinetic energy can be derived. The kinetic energy K of an object, then, is a scalar defined as follows, where m is the mass of the object and v is its velocity:
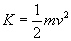
As it turns out, the kinetic energy is the work done on an object by the net force on that object. Thus, although a woman may do a certain amount of work on an object by lifting it from one height to another, the net force on that object is zero (the woman applies a force equal to but opposite in direction of gravity). Thus, there is no change in kinetic energy. If that object is released and allowed to fall, however, it gains kinetic energy because the net force on it is simply that of gravity (a single force). Thus, to understand the relationship of kinetic energy and work, we must refine our concept of work somewhat. If we define the work W as the total work done on the object by all forces (in other words, the work done on the object by the net force), then the following relationship between the work W and the initial and final kinetic energies (Ki and Kf) holds.
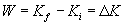where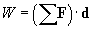 
Thus, the net work done on an object is equal to the change in that object's kinetic energy (?K). The following practice problems provide you with an opportunity to test and apply your understanding of the concepts of work and kinetic energy.
Practice Problem: A projectile of mass 1 kilogram travels at 5 meters per second. What speed must a 0.1-kilogram projectile travel to achieve the same kinetic energy?
Solution: First, let's calculate the kinetic energy of the more massive (1 kilogram) projectile.
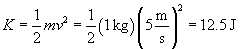
We can now calculate the speed of the less massive object such that it has this same kinetic energy, K.
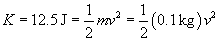
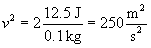
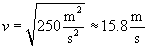
Practice Problem: A man lifts a 15-kilogram weight to a height of two meters off of the ground before dropping it. In the instant before the weight makes contact with the ground, what is its speed?
Solution: Let's draw a diagram illustrating the forces acting on the object as it is lifted and as it falls; these forces include gravity (Fg) and the upward force that the man applies (Fu).
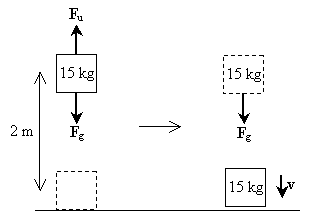
Note that the first step of the process (lifting the weight) involves no net force acting on the object--the force due to gravity is balanced by the force that the man applies in lifting the weight. In the second step, however, the weight only experiences the force of gravity. The net force, in this case, is therefore mg in the downward direction. As such, the velocity of the object is also in the downward direction. The work done on the weight as a result of gravity is simply mgh; this is also the total work done on the weight throughout the process. Note that the initial kinetic energy of the weight is zero because it has zero velocity. Let's now calculate the velocity by applying the relationship between net work and the change in kinetic energy.
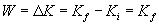
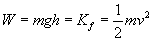
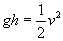
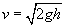
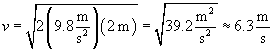
Thus, the velocity is about 6.3 meters per second. Note that the mass of the object has no part in the calculation-this result is the same regardless of the mass. (Also note that because of this result, if you drop any two objects-regardless of their masses-they will hit the ground at the same time.)
