The Relationship Between Geometry and Trigonometry

Trigonometry is an area of mathematics that studies the relationships of angles and sides of triangles. This article provides deeper insights into both the properties of circles and the properties of triangles (specifically, right triangles). By understanding just the basic aspects of trigonometry presented here, you will vastly expand your ability to solve geometry problems, and you will gain a foundation for studying more advanced mathematical topics.

Key Terms

o Trigonometry

o Sine

o Cosine

o Tangent (trigonometric function)

o Circular function

o Bisect

Objectives

o Understand the development of basic trigonometry from the properties of circles and right triangles

o Know how the basic trigonometric functions relate to the sides and angles of a right triangle

o Use trigonometric functions to calculate the lengths of chords in a circle

In this article, we will take a look at the relationship between right triangles and circles; this will allow us (in some cases) to find the lengths of chords as well as the lengths of certain sides of a triangle (regardless of whether it is a right triangle).

The Relationship Between Circles and Right Triangles

Consider a circle of radius r with a central angle α, such as shown below.

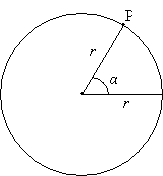
Let's draw a line segment from point P down to (and perpendicular with) the horizontal radius. This construction forms a right triangle with a hypotenuse of length r (the radius of the circle). Let's call the other two sides a (for the side adjacent to the angle α) and o (for the side opposite the angle α). We'll also rename the hypotenuse h (noting that h = r).

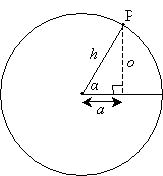
Recall from our study of triangles that two triangles sharing two congruent angles are similar, which in turn means that their sides are proportional. Thus, all right triangles with an angle of measure α are similar, and their sides are always proportional. As a result, the ratio of any two sides of a right triangle with a given angle α is constant, regardless of the length of the hypotenuse (radius of the corresponding circle, as above). Let's take a look at a diagram that illustrates this fact.

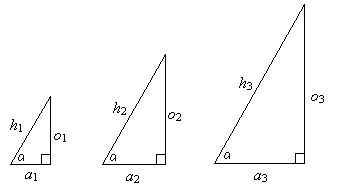
By the AA condition, the triangles above are all similar. Thus, the ratios of the corresponding sides of any two triangles are equivalent (in other words, the corresponding sides of any two similar triangles are proportional). For instance,

Here, k is simply the constant of proportionality. (For instance, one triangle might have sides that are all twice as long as those of another similar triangle--in such a case, k = 2.) So what does this all mean? It simply means that we can attempt to determine the relationship of the angle to the lengths of the sides of the triangle in the circle above without needing to know the radius of the circle. We can simply call the radius r--we do not need to know a specific value for r. Furthermore, because of the similarity of the triangles (such as those shown above), we can also show that the ratio of two sides in one particular triangle is equal to the ratio of two sides in another similar triangle. Again referring to the similar triangles above, we can thus say (for instance) that

Note that we can prove this to be true because corresponding sides of similar triangles are proportional:

We have thus shown that the ratio of two sides of a right triangle with a given interior angle α is the same regardless of the lengths of the sides. This is a crucial fact; if you are not sure why this is the case, it behooves you to reread the above derivation. If the derivation is clear to you, then you have taken your first step into understanding trigonometry, which is the study of the relationships among the angles and sides of a triangle. We will not delve deeply into trigonometry, but a basic understanding thereof is extremely useful in geometry.

Interested in learning more? Why not take an online Geometry course?

Let's go back to our right triangle formed by a central angle α in the circle of radius r. We know that the ratio of any two sides (a, o, or h) is a constant regardless of the particular value of r. This ratio does, however, depend on the angle α. Consider the ratio of o to a (that is, ); note in the diagram below that this ratio differs depending on the angle α. The ratio increases in magnitude from a small number of the left (a is larger than o) to a large value on the right (o is larger than a).

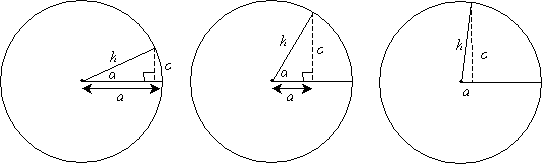
Thus, the ratio of any two sides in the right triangle depends on the angle α, but (again) not on the radius r. Because there are three different sides in the triangle, there are fundamentally three different ratios: the ratio of o to h, the ratio or a to h, and the ratio of o to a. Remember, these ratios all depend on the angle α. Three functions of α corresponding to these ratios: sine (sin), cosine (cos), and tangent (tan). These functions are defined as follows.

You can remember these relationships using the mnemonic term sohcahtoa (Sine is Opposite over Hypotenuse, and so on). Thus, if we know a particular value of the angle α, then we know these three ratios. You may at this point be wondering how we can calculate sines, cosines, and tangents--the answer is we need to use a calculator or, if you don't have a calculator, a table of values. A scientific calculator will generally have sine, cosine, and tangent functions available; some simpler calculators may have these functions as well. For certain angles, the trigonometric functions are rational values; for other angles, they are irrational values, and some approximation is therefore necessary when working with decimals or fractions.

An entire course could be devoted to the study of trigonometric functions (such as sine, cosine, and tangent). We will not delve much further into these functions other than to note their usefulness in relating the angles and sides of right triangles. It is also noteworthy that these functions are sometimes called circular functions, because of their relationship to the angle α in a circle. Again, however, we will not study these functions in any greater depth.

Practice Problem: Use a scientific calculator or table of values to find the following.

sin 45° cos 60° tan 0°

Solution: This problem simply provides you with the opportunity to calculate several values for trigonometric functions. If you are not getting the answers below, check to be sure that your calculator is in degree mode (or that the table of values corresponds to angle measures in degrees). If you are unsure, consult your calculator's user manual.

sin 45° =

cos 60° = 0.5

tan 0° = 0

Practice Problem: For each trigonometric function listed below, use the following diagram to find an equivalent expression in terms of a, b, and c.

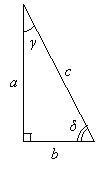
sin δ tan γ cos γ cos δ

Solution: Recall the mnemonic term for the relationship of the sides of a right triangle to a specific acute angle: sohcahtoa. Also be sure to note that the terms opposite and adjacent apply to the angle referenced in the trigonometric function. For the figure above, this means that the opposite side could be either a or b depending on which angle is referenced. Otherwise, these trigonometric functions only involve simple application of what we learned here.

Applying Trigonometry to Circles

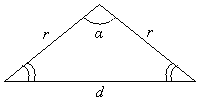
Now, we want to take what we have learned and apply it to circles. Let's calculate the length of a chord subtended by an angle α in a circle of radius r, as shown below.

Obviously, we have an isosceles triangle with two sides of length r and one side (the chord) of length d. Let's analyze this triangle to see if we can find d. Note that the two angles adjacent to the side d are congruent because the triangle is isosceles.

Now, let's construct a line segment from the apex of the triangle down to the opposite side such that the angle α is bisected (that is, cut in half). This creates two new angles each of measure α/2. The two newly formed triangles are congruent (we know this by the ASA condition). As a result, the side d is divided exactly in half by the new segment, and the new segment forms two right angles (that is, it is perpendicular to segment d).

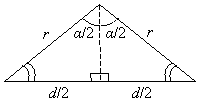
Now that we have a right triangle, we can use our trigonometric (trig) functions. The ratio of the side opposite the angle α/2 (that is, d/2) to the hypotenuse (that is, r), is the sine of the angle α/2. Thus, we can write the following.

Let's solve for d.

So, if we know the radius r of the circle and the angle α that subtends the chord, we can find the length of the chord. Let's consider an example. Assume the angle α is 60° and the circle has a radius of 1 foot. The length d of the corresponding chord is then the following.

Using a scientific calculator or table of values, we find that

Thus, the chord is 1 foot long, and we have just shown the usefulness (in this case) of trigonometry to geometric analysis. The following practice problem will allow you to apply what we have learned about circles and trigonometry to a similar situation.

Practice Problem: Find the area of the shaded region, where r is 3 inches and α is 75°.

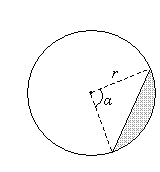
Solution: To solve this problem, we must apply a number of different concepts. The area of the shaded region is the difference between the area of a sector formed by a 75° central angle in a circle of radius 3 inches and the isosceles triangle with two sides of length 3 inches and an included angle of 75°. Let's first find the area of the sector, which we'll call S-we can use the following formula. The area of the circle is A.

Now, let's find the area of the triangle. We'll draw a bisector of the angle α to form two right triangles. We can then use our trig ratios to find the lengths of the base and height of the triangle. We'll call the base length d and the height h.

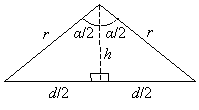
We know that r is 3 inches. We can use the cosine ratio to find h:

A good check of this result is to note that it is less than the radius--obviously, if it were to exceed the length of the circle's radius, it would be an incorrect result. So, we know the height of the triangle. Now, let's calculate the base using the sine ratio.