Key Terms
o Spurious solution
Objectives
o Practice applying algebra to the solution of problems in geometry
o Hone your ability to correctly assign variables and construct equations
Algebra in Geometry
Application of algebra to geometry essentially involves the use of variables, functions, and equations to represent various known or unknown aspects of, for example, geometric figures. To apply algebra in this context, you don't need any new algebra skills, but you do need to have some understanding of geometry and an ability to translate the somewhat abstract ideas of algebra to a more concrete use in geometry. Let's start with a couple of practice problems to illustrate.
Practice Problem: Find the perimeter of the following figure if the rectangle has an area of 63 square units.
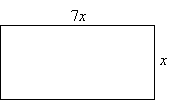
Solution: We know from basic geometry that the area of a rectangle is the product of the length and the width. In this case, the length is 7x and the width is x. The problem statement tells us that the area of the rectangle is 63 square units; we can use this fact to construct an equation in the variable x, which we can then solve for x.
A = lw
63 = (7x)(x) = 7x2
This is a quadratic equation, and we have learned numerous ways of handling this type of equation. Let's use the factoring approach (other approaches are perfectly legitimate, however).
7x2 – 63 = 0
x2 – 9 = 0
(x – 3)(x + 3) = 0
We can thus see that x is either +3 or –3; the negative value makes no sense in this context, however, so we reject it as a spurious solution (a solution that does not make any sense in the context of the problem). This leaves us with x = 3 units. Let's check to see if this value works to get the area:
A = (7)(3)(3) = 63
Now, we must find the perimeter of the rectangle, which is what the question is asking for. The perimeter is simply the sum of the lengths of the four sides of the rectangle.
P = 2l + 2w = 2(3) + 2(3)(7) = 6 + 42 = 48
The perimeter of the rectangle is thus 48 units. A slightly more rigorous version of this problem would ask you to find the perimeter of a rectangle with an area of 63 square units and with a length that is seven times the width. This question statement would force you to assign the variable in addition to solving the problem.
Practice Problem: Find the area of the shaded region in the figure below, where O is at the center of the circle and the inset square, and r is equal to 
.
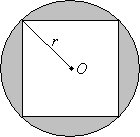
Solution: This problem is a bit more complicated than the previous one. We want to find the area of the shaded region; let's first figure out what we know. We know how to calculate the area of a square of side l and a circle of radius r:
Areacircle = πr2
Areasquare = l2
The area of the shaded region is simply the difference between the area of the circle and that of the square. In the figure, r is both the radius of the circle and half the diagonal of the square. Because r is specified, we can already calculate the area of the circle.
Areacircle = 
To find the solution to the problem, we now need to find the area of the square. We can see that the diagonal of the square is equal to the diameter of the circle, which is 2r or 
. We will need to use the Pythagorean theorem to find the length of the side of the square, which we will call x. We can use the following diagram to illustrate.
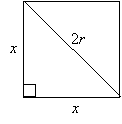
The Pythagorean theorem tells us that the sum of the squares of the two legs of a right triangle is equal to the square of the hypotenuse. In this case, the legs of the right triangle are both of length x and the hypotenuse has a length 2r. We can thus write this expression as follows:
Let's substitute the known value of r and solve for x.
Once again, we can reject the negative number as a spurious solution. The result is that the square has sides of length 4 units. The total area of the square is then 16 units. Let's use this to find the area of the shaded region.
Areashaded = Areacircle – Areasquare = 8π – 16 ≈ 9.13
The area of the shaded region is thus about 9.13 square units.
These two practice problems have shown us how algebra can be instrumental in solving a range of problems in geometry. Of course, a certain level of knowledge about the field of geometry is needed to do these problems, but the main point that you should come to realize is that algebra can indeed be useful in other fields of mathematics (and, particularly in this case, geometry). The crucial skill is the ability to appropriately assign variables or unknowns and to correctly construct equations that can be solved to find those variables or unknowns. Let's try another practice problem.
Practice Problem: Circle A has a circumference that is 10 times larger than circle B. If the radius of circle A is 
, what is the radius of circle B?
Solution: Let's start by drawing a diagram so that we can keep straight the information presented in the problem. We know that circle A is larger than circle B; there is no need to try to make the drawing to scale at this point. We know the radius of circle A, but we don't know it for circle B: let's call this radius r.
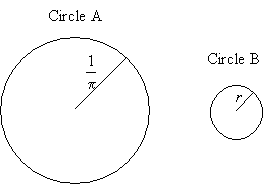
We can now calculate the circumference of circle A and write an expression for the circumference of circle B. (Recall that the circumference of a circle is 2π times the radius.)
CA = 
CB = 2πr
We are told in the problem that the circumference of circle A is 10 times that of circle B. We can then write an equation that we will solve for r.
CA = 10CB
2 = 10(2πr) = 20πr
r = 
Thus, the radius of circle B is one-tenth that of circle A.
