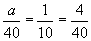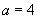Key Terms
o Decimal
o Irrational number
o Rational number
o Percent
o Ratio
o Proportion
Objectives
o Recognize a decimal and know how to convert from decimals to fractions (and vice versa)
o Recognize percents and understand their relationship to decimals, fractions, and ratios
o Understand the meaning of a ratio (proportion) and be able to use it in simple cases
Decimals
As you have probably noticed, most basic calculators (as well as many more-advanced calculators) do not deal with fractions. If you divide 3 by 4, for instance, you will not get a result of 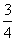 ; instead, you will get 0.75. This representation of a non-integer number is called a decimal. Converting from a fraction to a decimal is a simple matter of performing the long division (or, in some cases, just using a calculator). The example of
; instead, you will get 0.75. This representation of a non-integer number is called a decimal. Converting from a fraction to a decimal is a simple matter of performing the long division (or, in some cases, just using a calculator). The example of 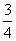 is shown below for the purposes of illustration. Note that careful track must be kept of the decimal point when performing this type of division.
is shown below for the purposes of illustration. Note that careful track must be kept of the decimal point when performing this type of division.
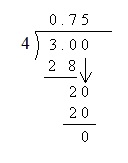
In some instances, a fraction cannot be written as a decimal with a finite (limited) number of decimal places. Consider, for instance, 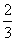 . Let's look at a portion of the long division for this fraction.
. Let's look at a portion of the long division for this fraction.
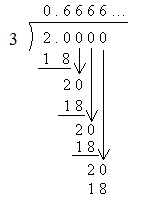
Clearly, the long division will continue indefinitely, adding additional sixes to the decimal without end. Such repeating decimals are occasionally written as, in the case of this example, 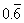 . The bar indicates that the 6 repeats unendingly. A decimal
. The bar indicates that the 6 repeats unendingly. A decimal 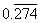 is the same as 0.274274274274.
is the same as 0.274274274274.
Converting a decimal to a fraction can be somewhat simpler (as long as the decimal is not repeating, although even repeating decimals can be converted to fractions-it just requires a bit more work). Consider the decimal 0.582, for instance. If we multiply this decimal by 1,000, we get 582:
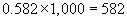
Concomitantly, we can divide 582 by 1,000 to get 0.582.
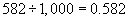
But we can also write this division operation as a fraction:
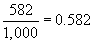
Reducing to lowest terms yields the following result.
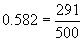
Generally, given some decimal, we can convert to a fraction by writing in the numerator the decimal, less the decimal point, and by writing in the denominator 1 followed by the same number of zeroes as the number of decimal places. Let's consider another example: 0.64. The fraction corresponding to this decimal would have a numerator of 64 (we eliminate the decimal point) and a denominator of 100. The operation of dividing 64 by 100 actually takes the decimal point (which is located next to the 4--64.0) and moves it to the left two places, leaving 0.64.
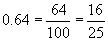
This approach works for any fraction with a finite number of decimal places, even those that include some number to the left of the decimal point. For instance,
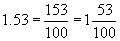
Decimals with an infinite number of decimal places but no repeating pattern cannot be converted to a fraction with an integer numerator and integer denominator-these numbers are called irrational numbers. Any decimal that can be converted to a fraction with an integer numerator and integer denominator is called a rational number; repeating decimals (even though they have an infinite number of decimal places) and decimals with a finite number of decimal places are all rational numbers. The following practice problems provide you with the opportunity to practice converting fractions to decimals and vice versa.
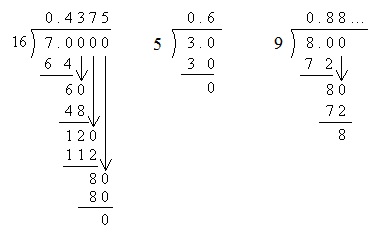
Practice Problem: Convert each fraction to a decimal.
a. 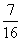 b.
b. 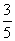 c.
c. 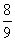
Solution: In each case, do the long division of the numerator divided by the denominator. In part c, note that the decimal repeats-you need only perform a couple steps in the division to recognize this repetition.
a. 0.4375 b. 0.6 c. 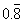
Practice Problem: Convert the following decimals to fractions.
a. 0.932 b. 0.34 c. 1.52
Solution: Follow the procedure outlined in the discussion above. Reduce to lowest terms when possible.
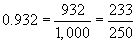
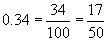
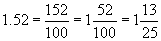
Percents
You probably have heard the word percent used in casual conversation and perhaps even in some slightly more mathematical contexts. For instance, someone might say, "I am giving 100 percent to the job," or "the sales tax rate is 5 percent." In each of these instances, the figure referred to using the term percent refers to some portion of a whole amount. For instance, 100 percent refers to an entirety-someone who is "giving 100 percent" is "giving it his all." The term percent actually means "per hundred," and it is often represented using the symbol %. Thus, 100% and 100 percent are the same thing. A percent is thus a fraction (note how the symbol % looks suspiciously like a fraction!) where the number before the symbol represents the portion per hundred. Thus, for example, 50% of the apples is the same as 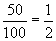 of the apples. Percents can be any number, whether positive or negative.
of the apples. Percents can be any number, whether positive or negative.
To convert from a percent to a regular number, simply divide the percent by 100. Depending on the context, a decimal or a fraction may be the appropriate representation. If a fraction is best, write the percent in the numerator and 100 in the denominator, then reduce to lowest terms. If a decimal is best, simply move the decimal point of the percent to the left by two places (the same as dividing by 100). To convert from a regular number to a percent, simply multiply by 100%. Thus, for instance, 0.25 is the same as 25%, and 98% is the same as 0.98 and 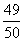 .
.
Practice Problem: Convert each fraction to a percent.
a. 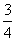 b.
b. 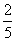 c.
c. 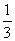
Solution: To convert to a percent, multiply by 100%. Percents can be written as fractions, but they are typically written as decimals. In part c, you can do the long division and write the percent using the bar notation discussed above.
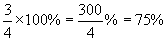 b.
b. 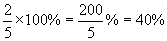
c. 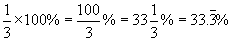
Practice Problem: Convert each percent to a fraction in lowest terms.
a. 80% b. 35% c. 12.5%
Solution: In each case, divide by 100% and reduce to lowest terms. To get rid of the decimal in part c, simply multiply both numerator and denominator by 10 (recall that this is the same as multiplying the fraction by 1).
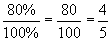 b.
b. 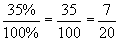
c. 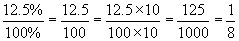
Percents and Ratios
A percent is not (necessarily) a strict count of, for example, some number of objects. That is, 50% of a basket of apples is not necessarily equal to 50 apples. The expression 50% means half the apples-thus, if the basket contains 24 apples, 50% of the apples is 12. Thus, a percent is actually a ratio (or proportion), which is a relationship between two quantities. In the case of our example, we are considering 12 out of 24 apples. For instance, we might be looking at the number of apples that are bad or the number that exceed a certain size. In either case, we are considering the relationship between one number (12 apples of a certain size or quality, for instance) and another number (24 apples-the entire lot in the basket). Ratios can be expressed in words (12 out of 24) or using a colon (12:24) or as a fraction (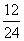 ). Because the representation as a fraction is equivalent to the other representations, we can reduce the ratio to lowest terms (in other words,
). Because the representation as a fraction is equivalent to the other representations, we can reduce the ratio to lowest terms (in other words, 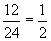 ). Thus, 12 out of 24 is the same as 1 out of 2, just as 12:24 is the same as 1:2.
). Thus, 12 out of 24 is the same as 1 out of 2, just as 12:24 is the same as 1:2.
A percent is therefore a specific kind of ratio where the number to which we are comparing is 100. Thus, the ratio 12:24 (or 1:2) is the same as 50%. Simply remember that the first number in a ratio (given in any of the above-mentioned forms) corresponds to the numerator of a fraction, and the second number corresponds to the denominator. Using the rules that we have studied so far, you should then be able to convert between ratios, fractions, percents, and decimals.
Practice Problem: Write each number or percent as a ratio using colon (:) notation (in lowest terms).
a. 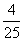 b. 48% c. 1.75
b. 48% c. 1.75
Solution: Remember that a ratio (using colon notation) is the same as a fraction, where the first number is the numerator and the second the denominator.
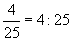 b.
b. 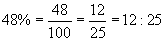
c. 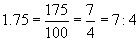
Using Ratios (Proportions)
The ability to use ratios (or proportions) is a crucial skill in algebra. Proportions allow us to talk about relative amounts; for instance, we might talk about performance on a test as a proportion of questions answered correctly. If we know that a student correctly answers 95% of the questions on a test, we have a good indication of her performance regardless of whether we know how many questions were on the test. If we do know this number, though, we can also determine how many she answered correctly. Let's say the test had 200 questions. We know, then, that the quotient of the number answered correctly divided by 200 is equal to 95% (or 0.95, or 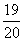 ).
).
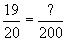
The expression above uses a question mark (?) to represent the unknown quantity, but we can also use another symbol corresponding to an unknown quantity. For instance, let's use x. The letter x is simply a placeholder for a value that is unknown or that can change.
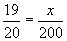
We now want to find x. One conceptually simple approach is to convert the fraction on the left into a fraction with a denominator of 200-the numerators of the fractions would then be required to be equal.
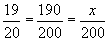
Thus, we see that x = 190. In other words, if the student scores 95% correct on a test with 200 questions, then she has answered 190 questions correctly. Note also that 190 is simply the product of the percent and the number of questions.
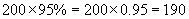
(Be careful when performing operations using percents. The best approach is to always convert a percent to a fraction or decimal before performing the operation.) The above discussion and example provides a glimpse at proportions and how to glean information from them.
Practice Problem: Find y to satisfy the expression below.
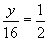
Solution: This expression equates two proportions. We can write the known proportion as an equivalent fraction with a denominator of 16; this allows us to easily find y.
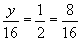
Thus, y = 8.
Practice Problem: An apple picker has learned from experience that 10% of all apples picked from a certain orchard have a worm in them. If she has a basket containing 40 apples, how many can she expect to contain a worm?
Solution: This word problem gives us the opportunity to apply what we know about percents and proportions. First, let's write 10% as a proportion.
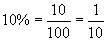
Now, we know that the apple picker has 40 apples in her basket, and we want to know how many she should expect to contain a worm. Let's say that the number of apples with a worm is a (remember, the use of a letter like a is just for the purposes of holding the place of the unknown number). The ratio of a to 40 (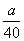 ) must be the same as the ratio of apples with worms to the total number of apples (
) must be the same as the ratio of apples with worms to the total number of apples (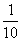 ). Let's therefore calculate a.
). Let's therefore calculate a.