Key Terms

o         Real number

o         Complex number

o         Natural number

o         Rational number

o         Irrational number

o         Commutativity

o         Associativity

o         Distributivity

o         Identity

o         Inverse

Objectives

o         Learn what is the set of real numbers

o         Recognize some of the main subsets of the real numbers

o         Know the properties of real numbers and why they are applicable

Real and Complex Numbers

The numbers we deal with in the real world (ignoring any units that go along with them, such as dollars, inches, degrees, etc.) are usually real numbers. A real number is any number that can be placed on a number line that extends to infinity in both the positive and negative directions. This number line is illustrated below with the number 4.5 marked with a closed dot as an example. The set of real numbers is often referred to using the symbol .

The above illustration, of course, only shows a portion of the number line (it would be impossible to show the whole thing), and only certain numbers are labeled (–1, 0, 1, etc.). A real number can thus be 8, 4.357, –3/5, π, , or any other such number. The particular representation, whether it be a fraction, a decimal, or another representation, does not matter. Perhaps the best way to describe a real number is to identify numbers that are not real numbers. Infinity (∞) is not a real number, although it is greater than any given real number; also, is not a real number, since there is no number whose square is equal to –1.

As a brief aside, let's define the imaginary number (so called because there is no equivalent "real number") using the letter i; we can then create a new set of numbers called the complex numbers. A complex number is any number that includes i. Thus, 3i, 2 + 5.4i, and –πi are all complex numbers. (In fact, the real numbers are a subset of the complex numbers-any real number r can be written as r + 0i, which is a complex representation.) Complex numbers are an important part of algebra, and they do have relevance to such things as solutions to polynomial equations. The symbol  is often used for the set of complex numbers.

Subsets of the Real Numbers

Real numbers include a range of apparently different numbers: for example, numbers that have no decimals, numbers with a finite number of decimal places, and numbers with an infinite number of decimal places. Let's look at some of the subsets of the real numbers, starting with the most basic.

Children first learn the "counting" numbers: 1, 2, 3, etc. These are formally called natural numbers, and the set of natural numbers is often denoted by the symbol . If we add to this set the number 0, we get the whole numbers. In addition to positive numbers, there are also negative numbers: if we include the negative values of each whole number in the set, we get the so-called integers. The set of integers is often referred to using the symbol .

In addition to the integers, the set of real numbers also includes fractional (or decimal) numbers. There are an infinite number of fractional values between any two integers. Consider 1 and 2, for instance; between these numbers are the values 1.1, 1.11, 1.111, 1.1111, and so on. Obviously, we could add as many additional decimal places as we would like. The set of real numbers is divided into two fundamentally different types of numbers: rational numbers and irrational numbers. A rational number is a number that can be equivalently expressed as a fraction , where a and b are both integers and b does not equal 0. Rational numbers thus include the integers as well as finite decimals and repeating decimals (such as 0.126126126.). The symbol  is often used for the set of rational numbers. An irrational number, on the other hand, is a non-repeating decimal with no termination. The set of real numbers is composed entirely of rational and irrational numbers.

Practice Problem: Identify which of the following numbers belong to : {0, i, 3.54, , ∞}.

Solution: If a number can be written as where a and b are integers, then that number is rational (i.e., it is in the set ). Note the following:

Thus, each of these numbers is rational. The number i is imaginary, so it doesn't belong to the real numbers. Likewise, ∞ is not a real number; i and ∞ are therefore not in the set .

Properties of Real Numbers

Now that you know a bit more about the real numbers and some of its subsets, we can move on to a discussion of some of the properties of real numbers (and operations on real numbers). Although some of the properties are obvious, they are nonetheless helpful in justifying the various steps required to solve problems or to prove theorems. Remember: variables are simply unknown values, so they act in the same manner as numbers when you add, subtract, multiply, divide, and so on.

One property is that multiplication and addition of real numbers is commutative. Commutativity states that the order of two numbers being multiplied or added does not affect the result. We can write this symbolically below, where x and y are two real numbers (note that a . can be used in place of a to indicate multiplication):

Imagine that you have a group of x bananas and a group of y bananas; it doesn't matter how you put them together, you will always end up with the same total number of bananas, which is either x + y or y + x. Similarly, if you have a rectangle with length x and width y, it doesn't matter if you multiply x by y or y by x; the area of the rectangle is always the same, as shown below.

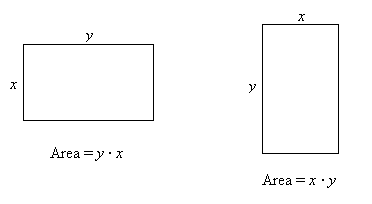
Another property, which is similar to commutativity, is associativity. Associativity states that the order in which three numbers are added or the order in which they are multiplied does not affect the result. If we consider real numbers x, y, and z, then

Recall that operations in parentheses are performed before those that are outside parentheses.

Distributivity is another property of real numbers that, in this case, relates to combination of multiplication and addition. This property is expressed below.

We can understand this property by again looking at groups of bananas. Let's say, for instance, that we have 3 groups of 6 bananas and 3 groups of 5 bananas. If we combine these groups one for one (one group of 6 with one group of 5), we end up with 3 groups of 11 bananas.

The last two properties that we will discuss are identity and inverse. The identity property simply states that the addition of any number x with 0 is simply x, and the multiplication of any number x with 1 is likewise x.

The property of inverses for a real number x states the following:

Note that the inverse property is closely related to identity.

These properties, by themselves, may seem a bit esoteric. Although when taken completely out of context they may seem to be less than useful, it does turn out that you will use them regularly, even if you don't explicitly acknowledge this in each case.

Practice Problem: Identify the property of real numbers that justifies each equality:

a + i = i + a; ; 5r + 3s - (5r + 3s) = 0.

Solution: In the first case, a + i = i + a, the equality is clearly justified by commutativity. For the second equality, we can also write it as follows:

Thus, this example illustrates the use of associativity. The last example is justified by the property of inverses.