Key Terms
o Divisible
o Integer
o Fraction
o Numerator
o Denominator
o Equivalent fraction
o Lowest terms
o Proper fraction
o Improper fraction
o Mixed number
Objectives
o Understand what a fraction is and recognize its parts
o Identify equivalent fractions
o Reduce fractions to lowest terms
o Recognize proper and improper fractions
o Convert between improper fraction and mixed number representations
What is a Fraction?
You may have noticed or considered that certain cases of division cause some difficulty. We do not have any problem dividing, for instance, 9 by 3 or 10 by 2. If we want to divide 12 by 5, for instance, then we run into trouble: 5 doesn't go into 12 evenly--the quotient is somewhere between 2 and 3! (We would therefore say that 12 is not divisible by 5. In some cases, the term evenly divisible is used.) But this type of division is not beyond what most people experience in daily life. For instance, a recipe might call for one and a half pounds of meat; a baker might have to cut a pie into eighths.
Integers are all the counting numbers (1, 2, 3, and so on), all the negative counting numbers (–1, –2, –3, and so on), and zero (0). Between any two integers (such as 0 and 1), however, is a whole world of numbers called fractions. When we talk about fractions, we will usually mean a number such as one-half (written 
), as opposed to the decimal notation 0.5. The term fraction, however, can also simply mean any non-integer number, whether it is expressed as a decimal or not.
As noted above, a fraction such as one-fourth is written as shown below. The top number is called the numerator, and the bottom number is called the denominator.
). Let's take a look at this relationship. Imagine one full circle; if we divide it into four (the denominator) equal pieces and take one (the numerator) of them, then we are left with one-fourth of the circle (the shaded portion).
4 (divide 1 whole circle four ways). Thus,
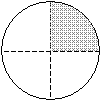
Below are some additional examples of fractions along with a representation of their meaning in terms of a portion of a circle.
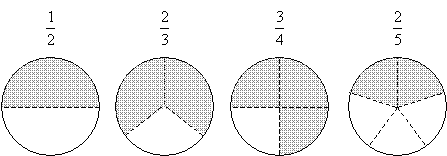
Equivalent Fractions and Lowest Terms
Certain fractions may look entirely different and yet actually correspond to the same quantity. For instance, let's take a look at our circle representations for the fractions 
and 
. Although these fractions look different, they are actually the same.
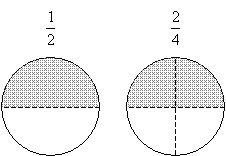
Both fractions correspond to exactly half the circle, but the numbers are different. Note that if we multiply both the numerator and denominator of 
by 2, we get 
. Likewise, following the same approach, we could also get 
if we multiplied numerator and denominator by 3, 
if we multiplied by 4, and so on. In each case, the fraction is equal to 
, however. To further illustrate, the case of 
is shown below.
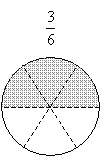
Consequently, if we look at this process in reverse, then we can obtain an equivalent fraction by dividing both numerator and denominator by the same number. We can do this as many times as we like-as long as we always divide both the numerator and denominator by the same number, we will always end up with an equivalent fraction that represents the same quantity as the original fraction.
Practice Problem: Determine if the following pairs of fractions are equivalent.
a. 
and 
b. 
and 
c. 
and 
d. 
and 
Solution: In each case, we can determine if the fractions are equivalent by checking to see if the same number multiplied by both the numerator and denominator of one fraction gives us the other fraction. For instance, in part a, if we multiply both the numerator and denominator of 
by 3, we get 
. Thus, these fractions are equivalent.
A more focused approach is, for instance, to divide the larger of the two denominators by the smaller and then multiply the quotient by the numerator of the second fraction (the one with the smaller denominator). If this product is equal to the numerator of the first fraction (the one with the larger denominator), then the fractions are equivalent. In part b, 10
5 is 2; if we multiply the numerator of 
(the fraction with the smaller denominator) by 2, we get 6. Because 6 ≠ 7, however, the fractions are not equivalent.
Using the same approach (or another similar approach, or simply inspection), we can show that the fractions in part c are not equivalent, but the fractions in part d are equivalent.
Because the fractions 
and 
(for instance) are equal, we can benefit from a way to express equivalent fractions in a simple standard form (intuitively speaking, 
is simpler than 
). This standard form is called lowest terms, and it is the equivalent fraction whose numerator and denominator do not share any common factors. Another way of saying this is that there is no integer by which the numerator and denominator are both evenly divisible. For instance, the fraction 
is in lowest terms because there is no integer by which both 1 and 3 are evenly divisible. (We ignore the divisor 1 because
1
1 = 1 and 3
1 = 3-dividing numerator and denominator by 1 does not change the fraction.) On the other hand, the fraction 
is not in lowest terms because 100 and 300 are both evenly divisible by 100. If we perform this division, we are left with an equivalent fraction (
) in lowest terms.
Practice Problem: Determine if each of the following fractions is in lowest terms. If not, find the equivalent fraction in lowest terms.
a. 
b. 
c. 
d. 
Solution: In each case, determine if the numerator and denominator are both evenly divisible by some integer. If not, then the fraction is in lowest terms. If both are divisible by some integer, perform the division and repeat the process until the fraction is in lowest terms. The basic process is shown for each case below.
b. 
is in lowest terms.c. 
d. 
is in lowest terms
Proper and Improper Fractions
, 
, and 
. Don't be fooled by the terminology-there is nothing morally or functionally "improper" about using improper fractions! An improper fraction is a perfectly legitimate way to represent non-integer numbers greater than one (or less than negative one). The only "improper" feature of the fraction is that its numerator is greater in magnitude than its denominator. Using improper fractions, we can write a mathematical expression for cases such as the following.
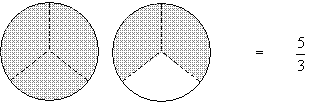
Note in the above case that what we have is a full circle plus two-thirds of another circle. In other words,
If we simply omit the plus sign, then we have expressed the improper fraction as a mixed number. A mixed number, which is shown below for the above example, is simply an equivalent representation consisting of an integer followed immediately by a proper fraction.
Practice Problem: Write each of the following improper fractions as a mixed number in lowest terms.
a. 
b. 
c. 
d. 
Solution: To find the mixed number representation of the fraction, perform the (remainder) division of the numerator by the denominator-the integer portion of the quotient is the integer portion of the mixed number. The fraction of the mixed number is the remainder of the above division over the denominator of the fraction. For instance, in part a, 9
5 is 1 with a remainder of 4. Thus,
The remaining parts can be solved in the same way. (Note in part c the result is simply an integer-the numerator of the fraction would be zero, so it is omitted. Part d requires that we reduce the fraction to lowest terms.)
b. 
c. 
d. 
Practice Problem: Write each of the following mixed numbers as an improper fraction.
a. 
b. 
c. 
d. 
Solution: This problem requires that we perform the conversion of improper fraction to mixed number in reverse. To do this, multiply the integer by the denominator and then add the result to the numerator. The result is the equivalent improper fraction.
b. 
c. 
d. 
