Key Terms
o Scientific notation
Objectives
o Derive the rules for multiplying and dividing exponential expressions
o Determine the meaning of a negative exponent
o Apply exponents to understanding and using scientific notation
Exponents are a way of representing repeated multiplication (similarly to the way multiplication is a way of expressing repeated addition). In some instances, we may need to perform operations on numbers with exponents; by learning some basic rules, we can make the process much simpler. These rules can be of great value in more advanced algebra when dealing with variables (or otherwise unspecified numbers) that have exponents.
The Rules of Exponents
Let's say we want to multiply two exponential expressions with the same base, such as ![]() and
and ![]() . The "brute force" approach to finding the product would be to expand each exponent, multiply the results, and convert back to an exponent (assuming an exponential representation of the result is desired).
. The "brute force" approach to finding the product would be to expand each exponent, multiply the results, and convert back to an exponent (assuming an exponential representation of the result is desired).
![]()
Note carefully that when we multiply two exponents (again, assuming they have the same base), the result is multiplication of the factors of the first exponent and the factors of the second exponent. The total number of factors is thus the sum of the two exponents. We can generalize this rule using letters to stand in the place of unspecified numbers.
![]()
You may often see the multiplication operation expressed using a dot (·) instead of a cross (![]() ), or you may see it expressed without any symbol at all. Thus, each of the following expressions is equivalent to the others.
), or you may see it expressed without any symbol at all. Thus, each of the following expressions is equivalent to the others.
![]()
We can derive a similar rule for division. Let's take a look at what happens when we divide ![]() by
by ![]() .
.
![]()
Now, we can "cancel" any instance of a factor that appears in both the numerator and denominator. Why is this the case? Recall that we were able to find equivalent fractions by multiplying (or dividing) both the numerator and denominator by a particular value-this is equivalent to multiplying or dividing by one. Thus, we can do the following:
![]()
This is nothing more than writing the original fraction in an equivalent form. Instead of the fraction involving a single number, it involves a series of operations (multiplication, in this case).
![]()
![]()
The simple way to look at this is that any factors in the numerator can simply cancel equivalent factors in the denominator. Thus, for every instance where 2 appears in the numerator and denominator, we can cross that pair off.
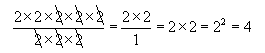

We can see that the exponent of the answer is the difference between that of the numerator and that of the denominator (again, all have the same base). Let's generalize the rule:
![]()
Let's consider one more case: what if an exponential expression is itself raised to an exponent, as with the example below?
![]()
Expand the expression to see what it looks like in terms of multiplication.
![]()
Notice that the expression in parentheses has three factors, and we must multiply this expression four times. Thus, the total number of factors of two is 12, or the product of the exponents. Generally, the rule can be stated as follows.
![]()
The key to using these rules is to note that the exponential expressions must always have the same base-the rules do not apply to exponents with different bases. To recap, the rules of exponents are the following.
![]()
Practice Problem: Write each of the following as an exponential expression with a single base and a single exponent.
a. ![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()
Solution: In each case, use the rules for multiplying and dividing exponents to simplify the expression into a single base and a single exponent. Note in part c that any number is equal to itself raised to the first power. Note also the usefulness of these rules of exponents in part d: multiplying 150 twenty (or twenty-six) times is a tough proposition, and even most calculators cannot provide an exact product. The use of exponents, however, allows us to have an exact representation of the result.
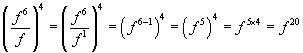
We now look at a slightly different case: a product of two (or more) factors, all raised to an exponent. Let's consider the example below.
![]()
Expand the exponential in the usual manner:
![]()
Notice that the expanded form has four factors of 2 and four factors of 3. This expression is the same as the following (multiplication is commutative, so we can rearrange the factors in the product).
![]()
Thus, given the product ab (or ![]() ), we can write the following general rule:
), we can write the following general rule:
![]()
Negative Exponents
If you consider division of exponential expressions, you may notice that the rule seems to indicate that we can end up with negative exponents. The following example, similar to an example above, illustrates this point:
![]()
But the rules of exponents indicate the following:
![]()
The results should be the same; so, let's equate the two and see what information we can glean from the result.
![]()
Let's rewrite the exponential expression as follows.
![]()
But the rules of exponents allow us to write this expression as an exponent raised to another exponent.
![]()
![]()
This result implies that an exponent of –1 is associated with the reciprocal:
![]()
Thus, any number a raised to the power of –1 is equal to ![]() .
.
![]()
Using our rules of exponents, therefore, we can determine generally what it means to raise a number to a power that is a negative number (specifically at this point, a negative integer). The derivation below follows the pattern of the example we considered above.
![]()
![]()
This result can be combined with the result we obtained previously for a product raised to a given power:
![]()
Let's consider a quotient (fraction) raised to a power. We can use the exponent rules we have studied thus far to derive an equivalent result. First, we'll use the above product rule as shown below.
![]()
Now, we'll use a negative exponent and other exponent rules.
![]()
Remember that multiplication is commutative. Thus,
![]()
Rewrite the second exponential as follows.
![]()
Thus, we obtain a rule for quotients similar to that for products:
![]()
Thus, we are now able to handle any integer exponents, whether positive or negative. We also know how to multiply and divide exponential expressions. Later in the course, we will consider fractional exponents. (As it turns out, fractional exponents obey the same rules as integer exponents, but the precise meaning of a fraction will be made clear later on.)
Practice Problem: Evaluate or simplify each expression.
a. ![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()
Solution: Use the rules of exponents along with the fact that a negative exponent indicates that the reciprocal of the base must be taken.
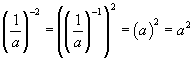 b.
b. c. 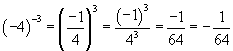 d.
d. 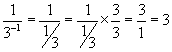
Application of Exponents: Scientific Notation
Although exponents may at times seem like an obscure or less than practical mathematical tool, they have numerous important and practical applications. For instance, exponents are used in so-called scientific notation, which is a way of representing decimal values that are very large or very small. Consider the two numbers below.
137,000,000,000,000,000,000,000,000
0.000000000000000000000137
Because of their sizes, writing these numbers is extremely cumbersome. If we could write them simply as 1.37 followed by some indication of the number of zeroes that follow or precede these digits, we could make the process of expressing these numbers much simpler. Note that we can obtain the larger number by repeatedly multiplying 1.37 by 10 some number of times.
![]()
The expression on the right must include 26 factors of 10. But we know how to write multiple factors using exponents:
![]()
We can do likewise with the smaller number. In this case, 1.37 must be divided by 10 some number of times.
![]()
In this case, the denominator contains 22 factors of 10. Let's use what we know about negative exponents to write this in a form similar to the one we used above for the larger number.
![]()
Scientific notation is this method of representing numbers. The general format is a single integer digit followed by some number of decimal places, all multiplied by an integer power of 10. Let's take a look at two more examples of conversion from standard notation to scientific notation.
![]()
![]()
Note that the exponent can also be viewed as the number of places that the decimal point must be moved to the left (for positive exponents) or to the right (for negative exponents) when going from the standard number to scientific notation.
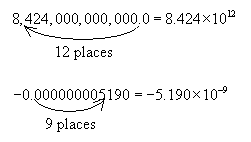

Practice Problem: Convert each number to scientific notation.
a. 0.0000041 b. –3,720,000 c. 0.0839
Solution: For each number, write a decimal containing the non-zero digits with the decimal point following the first digit, then multiply by the appropriate power of 10.
Practice Problem: Convert each number in scientific notation to a decimal in standard form.
a. ![]() b.
b. ![]() c.
c. ![]()
Solution: Conversion to standard form simply requires movement of the decimal point the number of places indicated by the exponent. For a negative exponent, the decimal point must be moved to the left, and for a positive exponent, it must be moved to the right.
c. ![]()