The Four Basic Mathematical Operations
Key Terms
o Term
o Sum
o Commutative
o Negative
o Difference
o Factor
o Product
o Dividend
o Divisor
o Quotient
Objectives
o Review addition, subtraction, multiplication, and division for positive and negative numbers
o Make note of the relationships between the operations
o Identify which operations are commutative
--addition, subtraction, multiplication, and division--have application even in the most advanced mathematical theories. Thus, mastering them is one of the keys to progressing in an understanding of math and, specifically, of algebra. Electronic calculators have made these (and other) operations simple to perform, but these devices can also create a dependency that makes really understanding mathematics quite difficult. Calculators can be a handy tool for checking answers, but if you rely too heavily on one, you may deprive yourself of the kind of rigorous mental exercises that will help you not just to do math, but to fully understand what you are doing.
If you have difficulty performing the basic operations for simple numbers, one way to improve is through the use of flash cards. Even cutting up a sheet of paper into sections is sufficient; just write the numbers and an operation on one side (such as 3
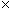 8) and the answer (24, for our example) on the other. In this way, you can practice your math skills without simply relying on a calculator. (But if you need the calculator to accurately make your flash cards, by all means, use one!) We assume you have an understanding of basic arithmetic, but if you are at all lacking in this area, you should be able to bring yourself up to speed with a little time and practice.
8) and the answer (24, for our example) on the other. In this way, you can practice your math skills without simply relying on a calculator. (But if you need the calculator to accurately make your flash cards, by all means, use one!) We assume you have an understanding of basic arithmetic, but if you are at all lacking in this area, you should be able to bring yourself up to speed with a little time and practice.Addition and Subtraction
Addition and subtraction are two complementary operations--we can actually define subtraction in terms of addition. Addition is simply the combination of distinct sets of like entities (and we must stress the word like). Thus, if we add one set of four squares to another set of five squares, we get a total of nine squares. (Or, if you prefer, substitute anything you like for "squares"--dogs, bananas, people, rocks, or anything else.)


The above diagram is an illustration of the process of addition. Note that the plus sign (+) indicates the operation performed on the two terms. In this case, the summands are four squares and five squares. The equal sign (=) indicates that what is on its left and what is on its right are equivalent (or equal). On the right side is the sum, which is the result of the addition of the summands. Of course, drawing pictures every time we wanted to represent an addition would be highly annoying (and in some cases impossible). Thus, instead of talking about a certain number of squares, apples, people, inches, or dollars) for instance, we can simply deal with the numbers.
4 + 5 = 9
Furthermore, note that the order in which we add the squares makes no difference. Whether we add four squares to five squares or vice versa, the result is always nine squares.
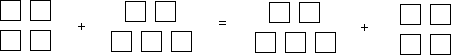

In mathematical parlance, addition is commutative; we can add two summands in any order and always get the same result. Following our example,
4 + 5 = 9
5 + 4 = 9
4 + 5 = 5 + 4
Subtraction is the opposite of addition. Instead of adding two quantities (numbers), we are removing one quantity from another. Thus, if we have nine squares and take away (subtract) five, we are left with four squares. Using just the numbers, where the minus sign (–) represents the subtraction operation,
9 – 5 = 4
Here, 9 and 5 are the terms of the operation, and 4 is the difference. Unlike addition, subtraction is not commutative. That is to say, 9 – 5 and 5 – 9 are not the same-in fact, they yield quite different results! (The symbol ≠ below simply means "does not equal.")
9 – 5 ≠ 5 – 9
Addition (and any other of the basic operations) can involve the counting numbers (1, 2, 3, 4, 5, and so on), the number zero (0), and any number in between (fractional values such as a half, for instance). Also, we may encounter negative numbers, which are quantities that are less than zero. If we think of positive numbers as quantities of something that we possess (say, for instance, that we have 10 oranges), then a negative number would be a quantity of something that we owe (if we owed someone 10 oranges, then we might say that we have negative 10 oranges). Negative numbers are typically expressed using a minus sign (–); thus, negative 10 can be written as -10. The use of the minus sign is no coincidence-in fact, subtraction is nothing more than addition involving a negative number! Imagine you have in your possession nine apples (positive nine), but you owe a friend four apples (negative four). Thus, you take four apples out of the nine that you have, leaving five.
9 – 4 = 5
9 + (–4) = 5
9 – 4 = 9 + (–4)
Multiplication and Division
Let's say we want to add a particular number, such as six, to itself many times. For instance, a worker at a factory may wish to count the number of parts delivered in several boxes. Each box contains six parts, and there are a total of five boxes. To find out how many parts he has, the worker must add the number six to itself five times.
6 + 6 + 6 + 6 + 6
We can find the sum simply by performing the addition several times over. A shortcut, however, is multiplication. Imagine the parts in each of the five boxes laid out in rows, as shown below (we use a square to represent a part).


Each row above represents a box; in each row is six parts. We have a total of five rows. Thus, instead of performing five additions of six, we simply multiply six by five to get a total of 30. Multiplication is typically represented by an 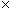 , although sometimes a · is used instead. The two numbers being multiplied are called factors, and the result is called the product.
, although sometimes a · is used instead. The two numbers being multiplied are called factors, and the result is called the product.
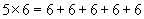
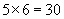
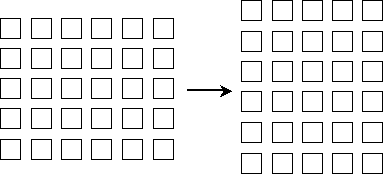
Like addition, multiplication is commutative. Imagine flipping the arrangement of squares shown above so that instead of being five rows of six squares each, it is six rows of five squares each. We haven't changed the total number of squares, but following the logic we've used, we can say that the total number of squares is now six multiplied by (or times) five.

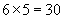
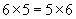
Multiplication of negative numbers carries with it some additional subtleties. Let's say someone owes a friend five apples; in some sense, he then has –5 apples. We can also look at this situation as that person owing his friend one apple five times over, which is –1 multiplied by 5. We already know that he has –5 apples, so the product of –1 and 5 must be –5.
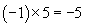
Thus, if one factor is positive and the other negative, their product is negative. What about the product of two negative numbers? We can view this as the "negation of a negation," or a double negative-the result is a positive number. (Imagine owing a friend a negative number of apples-that would be the same as having those apples in the first place!) For instance, then,
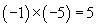
Division is the inverse of multiplication. For instance, imagine that the factory worker mentioned above has 30 parts and wants to distribute them among five boxes. He must divide 30 by 5; this operation is shown using the division symbol (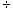 ).
).
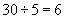
In other words, among the 30 parts, we can count 5 parts a total of 6 times. (Another way of saying this is that 5 goes into 30 six times.) The number being divided (30 in this case) is called the dividend, the number by which it is divided (5 in this case) is called the divisor, and the result is called the quotient. Recall that we wrote the following product:
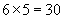
Note, then, that if the product of two factors is divided by one of the factors, the quotient is equal to the other factor.
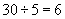
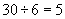
Division, unlike multiplication, is not commutative.
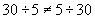
The rules for dividing negative numbers are the same as those for multiplication: if the dividend and divisor are both positive or both negative, the quotient is positive, and if one is positive and the other negative, then the quotient is negative. The following practice problems give you the opportunity to practice using some of the concepts discussed in this article.
Practice Problem: For each pair of expressions, determine if they are equal.
a. 3 + (–4) and (–4) + 3 b. 4 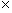 2 and 2
2 and 2 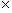 4 c. 3 – 1 and (–1) + 3
4 c. 3 – 1 and (–1) + 3
Solution: Each pair of expressions above is equal. Let's take a look at why this is the case. For part a, remember that addition is commutative. Thus, it doesn't matter what order we use for the terms, regardless of whether the numbers are negative or positive. The same reasoning applies to part b: multiplication is commutative. In part c, the two are also equal because subtraction is the same as addition of a negative:
3 – 1 = 3 + (–1)
Also, addition is commutative:
3 – 1 = 3 + (–1) = (–1) + 3
3 – 1 = (–1) + 3
Nevertheless, you must be cautious, because 3 – 1 is not equal to 1 – 3!
Practice Problem: Calculate each of the following.
a. (–5) + (–1) b. (–2)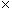 ( –5) c. 21
( –5) c. 21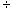 (–7) d. (–6) – (3)
(–7) d. (–6) – (3)
e. 4 + (–8) f. (–18) 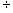 6 g. 4 – (–3) h. 9
6 g. 4 – (–3) h. 9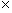 (–7)
(–7)
Solution: In each case, make careful note of the sign of the terms, factors, dividends, and divisors of the operations, being sure to follow the rules as laid out earlier. Parts a and b are straightforward.
a. –6 b. 10
If you cannot recall the rules for signs when dividing, remember that the product of the quotient and the divisor is the dividend. (In this case, the product of –3 and –7 is 21.)
c. –3
You can also rewrite part d using addition: (–6) – (3) = (–6) + (–3). The remainder of the parts follow the basic rules already discussed or the strategies we have reviewed for this problem.























