Introduction
In this article, we introduce the concept of a ray and discuss the laws of reflection and refraction.
Key Terms
o Ray
o Geometrical optics
o Reflection
o Angle of incidence
o Angle of reflection
o Law of reflection
o Index of refraction
o Law of refraction
o Relative permittivity
o Relative permeability
Objectives
o Describe the relationship between a wave and a ray
o Use the law of reflection to calculate the direction of reflected rays
o Define the index of refraction and its relationship with material parameters
o Use the law of refraction to describe the "bending" of rays as the pass from one material to another
Let's Begin!
Imagine electromagnetic radiation (light) emanating from a charged particle far away. The waves radiate symmetrically from the particle in concentric circles. The diagram below shows the waves moving outward from the source.
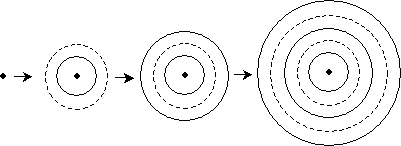

Notice that as the waves get farther away from the source, the curvature of the circle decreases. At a sufficiently large distance, the radius of the circle becomes so large that the wave appears (locally) as a line rather than a curve (in three dimensions, the wave appears to be a plane). For a so-called plane wave, all we need to know is the direction of travel, since the wave has a constant magnitude over the plane perpendicular to the direction. The diagram below shows a plane wave in two dimensions.
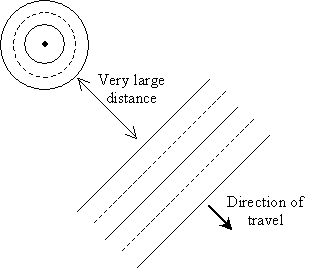

This direction of travel, because it is uniform all across the plane wave, is called a ray. To be sure, it is sometimes easier to imagine a ray as, for instance, a "ray" of sunlight or a laser beam. Although these analogies are not necessarily incorrect, the above definition is slightly more mathematically rigorous in the context of classical electromagnetics.
Now that we have something of a physical idea of what a ray is, we can turn to the topic of geometrical optics, which is the study of electromagnetic waves that can be approximated using rays. (A condition of geometrical optics is that the wavelength of the light be much smaller than the objects it encounters.)
Reflection and Refraction
Our study of geometrical optics will center on the application of two basic laws: one for reflection and one for refraction. Reflection is just as you might imagine: rays of light that are deflected by a surface (perhaps being sent back toward their source) are reflected. If you've ever looked in a mirror, you've looked at light that has been reflected by a surface (the mirror). Refraction is a slightly less intuitive concept, but it has an effect on everyday life. If you've ever noticed that a straw in a glass of water looks (from certain angles) like it is bent, or if you've ever seen a mirage on the road, then you've seen the effects of refraction. Refraction is the "bending" of light rays resulting from changes in the characteristics of the medium through which the rays are traveling. Two very simple formulas govern reflection and refraction in geometrical optics.
First, we consider reflection, as shown in the diagram below for a light wave striking a surface. We identify the incoming ray as the incident ray and the outgoing ray as the reflected ray. Concomitantly, the angle ?i that the incoming ray makes with a line (dashed in the diagram) normal to the surface is called the angle of incidence. The angle ?r for the reflected ray is called the angle of reflection.
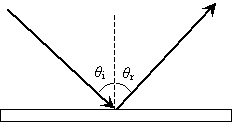
The law of reflection states that the angle of incidence is equal to the angle of reflection, or, stated mathematically,
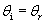
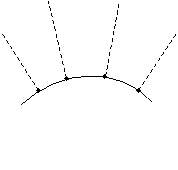
Although this relation is simple, you must always be careful to find the correct normal line that intersects the point of incidence. Although this is easy for a flat surface (it is just the line that is perpendicular to the surface), it is slightly more complicated for curved surfaces. Nevertheless, the same principle applies: the normal line is the line perpendicular to the surface at the point of incidence. Several normal lines are shown for different points on the curved surface below.
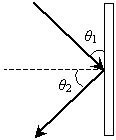
Practice Problem: A ray is incident on a mirror as shown below, where the dashed line is normal to the surface. What is the angle ?2 in terms of ?1?
Solution: The law of reflection states that the angle of incidence is equal to the angle of reflection (where both angles are measured from the normal line to the surface). The normal line is shown as the dashed line in the figure. Let's add angle ?3 to the figure; note that this angle is 90� - ?1.
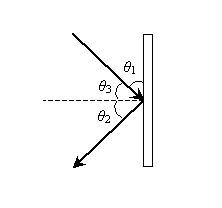

The law of reflection tells us that ?2 = ?3; on the basis of this and our conclusion about the relationship of ?1 and ?3, we can express ?2 in terms of ?1 as follows.
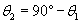
Practice Problem: Complete the diagram to show (approximately) the path of the ray upon reflection by the mirror shown below.
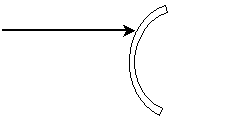
Solution: Earlier we learned that the angles of incidence and reflection are equal when measured from the line that is normal to the surface at the point of incidence. The first step to completing the diagram is to draw this normal line, thus allowing us to determine the angle of incidence, ?i. Because the problem asks us to find the approximate path of the reflected ray, we need not use a compass or other tool to perform an exact construction--we can simply "eyeball" the normal line and then the reflected ray.
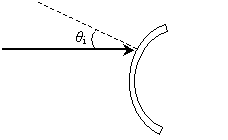
Now, let's draw the reflected ray.
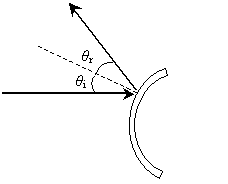
Using this technique, we can trace rays as they interact with multiple mirrors.
Next, we consider refraction. Refraction is the bending of light owing to a change in the characteristics of the material as the ray passes from one medium to another. The diagram below shows an example of a refracted ray with the angle of incidence ?1 in the first material and ?2 in the second material. (As with reflection, these angles are measured from the normal line to the surface.) Also, the first material has a so-called index of refraction n1, and the second material has an index of refraction n2.
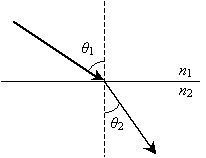

The law of refraction states the following:
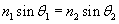
The law of refraction also states that the refracted ray is in the same plane as the incident ray. Thus, for instance, the refracted ray shown above cannot have a component of its direction that is into or out of the surface of the page. Before applying this law by way of practice problems, we shall briefly discuss the nature of the index of refraction, n. Recall that a vacuum has material parameters ?0 (the permittivity of free space) and ?0 (the permeability of free space). A material generally has a permittivity ? and permeability ?, where ? = ?r ?0 and ? = ?r ?0. (These different material parameters have an important effect on the speed of light; generally, the speed of light in a material with permittivity ? and permeability ? is 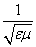 .) For a vacuum, the relative permittivity ?r is unity, as is the relative permeability ?0. These relative material parameters determine the index of refraction, n:
.) For a vacuum, the relative permittivity ?r is unity, as is the relative permeability ?0. These relative material parameters determine the index of refraction, n:
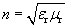
(Note, then, that the speed of light in a medium of index n is 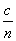 .) Thus, we further see that wave phenomena (rays, in this case) are closely linked to the electric and magnetic fields by way of these material parameters.
.) Thus, we further see that wave phenomena (rays, in this case) are closely linked to the electric and magnetic fields by way of these material parameters.
Practice Problem: A ray is incident from air (n ? 1.00) and passes into water (n ? 1.33) as shown below. What is the angle ?? (The normal to the surface is shown as a dashed line.)
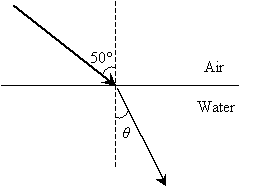
Solution: The law of refraction is expressed as follows, where the angles ?1 and ?2 are measured from the normal:
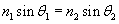
In this case, the ray starts in air (n1 = 1.00) at an angle ?1 = 50� from the normal and passes into water (n2 = 1.00), refracting with an angle ?2 = ? from the normal. Let's plug these numbers into the expression above and then calculate the result.
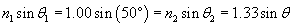
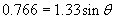
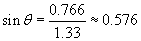
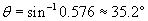
Thus, the refracted ray bends toward the normal by about 35� when passing from air (the material with the lower index) to water (the material with the higher index).
Practice Problem: What is the angle ? in the diagram below? (Assume the normal at the point of incidence intersects the horizontal dashed line at an angle of 30�.)
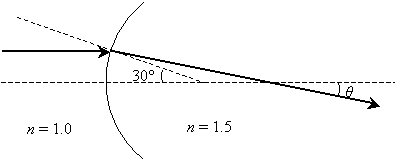

Solution: The ray is refracted by crossing a curved interface between two materials (possibly from air into glass). Notice that the incident ray is parallel to the horizontal dashed line--thus, the other dashed line (the normal at the point of incidence) intersects the incident ray at 30� (by the properties of corresponding angles of two parallel lines cut by a transversal line). We can use this result, which is shown below, to calculate ?, the angle of refraction.
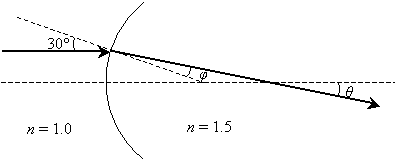

We can use the law of refraction to calculate ?.
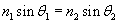
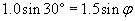
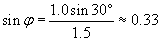
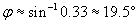
Now, we need to determine the relationship of the angle ? to the unknown angle ?. Because we know ?, we can use the fact that a triangle has 180� to calculate ?.
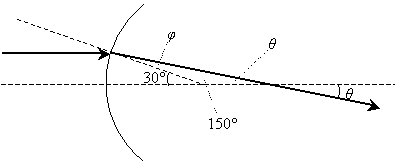

Note that we have calculated the obtuse angle in the triangle as 150�, because a straight line forms a 180� angle. The third angle of the triangle, which forms a vertical angle with ? (and is therefore congruent with ?), is 180� minus the sum of the other two angles (150� and ?).
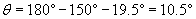
Thus, the angle ? is about 10.5�. This type of refraction problem sets the stage for a look at the action of lenses.