Math Skills: How to Do Multiplication

Grouping of objects

Although it is an oversimplification, multiplication can be seen as a quick form of addition. Let's go back to our idea of grouping objects to add them.

If we have four groups of three dogs:

We can count the dogs: 1, 2, 3, . . . 4, 5, 6 . . . 7, 8, 9 . . . 10, 11, 12

We can add the dogs: 3 + 3 + 3 + 3 = 12 (3 + 3 = 6, 6 + 3 = 9, and 9 + 3 = 12)

Or we can multiply: 4 x 3 = 12 which can be seen as ‘4 threes is 12'

Our multiplication problem can be written in one of three ways:

(a) 4 x 3 = 12

(b) 4(3) = 12

It should be obvious to you to if we are going to multiply numbers of more than one or two digits, we would want to line them up for place value as in example (c ).

Terms – Factor, Term, Product, Multiplier, Multiplicand, Times

Both numbers being multiplied (the 4 and the 3 in the example about the dogs) are called factors or terms. Sometimes one (or both) of them is referred to as the multiplier and the other is referred to as the multiplicand. The result or answer is the product of the multiplication.

16 factor, term, or multiplicand
x3 factor, term or multiplier

______

48 product

Both the sign used to designate multiplication, which is a lower case ‘x', and the whole operation are referred to as times. Therefore, we could say the ‘times problem' is "four times three" for ‘4 x 3.'

In many places you will see a dot (·) or a star or asterisk (*) used instead of a lower case ‘x.' Thus, the problem would be 4 x 3 or 4 · 3 or 4 * 3.

Multiplication Table

As with addition, learning some basic multiplication facts will make life much easier. In the table below you will find the numbers 0 through 9 across the top and again down the left side. To multiply 4 x 3, locate the four on the top row and the three along the left side and follow both until the row and column intersect. The number in that cell is 12.

We could also locate the 3 along the top row and the 4 along the left side. The intersection again would be 12. It does not matter in which order we multiply the factors.

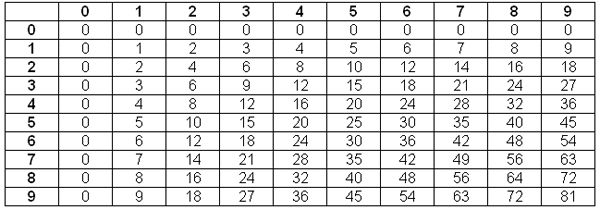
Flash cards are a great aid in learning multiplication facts.

Multiplication by zero

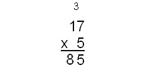
Want to learn more? Take an online course in Basic Math.

As you can see from the multiplication table, any number multiplied by zero is zero. If you have zero groups of things, then you have nothing – zero.

Multiplication with a single digit multiplier

The facts on the multiplication table are all factors that are single digits. You can also multiply a multiple digit number by a single digit number. We can multiply 5 x 7 or we can multiply 5 x 17. It is pretty simple to find and write the answer to 5 x 7 as 35; however, when we try to multiply 5 x 17, we find it is easier to line them up by place value because we will have to carry in this problem.

                    17
                    x 5
                  _____

We multiply 5 x 7 and get 35, so we write the 5 in the ones column and carry the 3 tens to the tens column.

Now we multiply 5 x 1 ten and get 5 tens, but we have 3 tens to add to that, so we really have 8 tens.

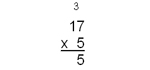
Multiplication with a multiple digit multiplier

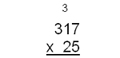
If both factors are multiple digit, we have extra steps. Let's say we want to multiply 317 by 25. Our first step will be to multiply 317 by 5 ones. The second step is to multiply 317 by 2 tens (20). And the final step is to add the two answers together.

We would start in just the same way as when we multiplied 17 by 5. The digit in the ones place of the multiplier is the starting point as we multiply the ones place by the ones place, or 5 x 7, and get 35. We put the 5 in the ones place of our answer and carry the 3 tens.

Then we multiply 5 x 1 ten and get 5 tens, and add the 3 tens to get 8 tens. We write the 8 in the tens place. Then we multiply the 5 x 3 and get 15. We can put the 5 in the hundreds place and the 1 in the thousands place. However, we are only part of the way done with our multiplication.

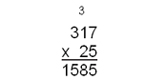
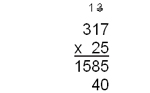
We now have to multiply the entire top term by the 2 tens, or 20. To designate that we are done with multiplying by the digit in the ones column and starting with the digit in the tens column and to help us when we get ready to add at the end, we will put a 0 in the ones column below the 5. Then we will multiply 2 x 7 to get 14. We now want to put the 4 in the tens column and carry the 1 to the tens column above because we really were multiplying 2 tens (20) times 7 which gave us 140. Be careful not to confuse the little numbers above each column that indicate what you are carrying. Some people cross out the number once they have added it.

Now multiply the 2 tens (20) times the 1 ten (10) and you get 20 tens which is 200. To this add the 1 hundred you have carried. This gives you a 3 (for 300) to place in the hundreds place. Then you can multiply the 2 tens (20) times the 3 hundreds (300) to get 6 thousands (6000).

Now you must add the two parts of your answer together to get the final answer. 5 ones + 0 ones is 5 ones. 8 tens + 4 tens is 12 tens (120), so put the 2 in the tens place and carry 10 tens or 1 hundred. 5 hundreds + 3 hundreds is 8 hundreds, plus the 1 hundred you carried is 9 hundreds. 1 thousand + 6 thousands gives you 7 thousands. Your final answer is 7,925.

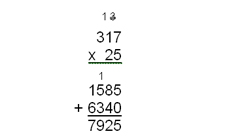
If the multiplier has a zero as one of the digits, do not forget to use a zero for a place holder. See example below.

Exponents

If a number is multiplied by itself, we can show this with an exponent. For example, if we want to multiply 5 x 5, we can show that as 5² which denotes two fives being multiplied. It is called ‘five squared' or ‘five raised to the second power. 'This is especially helpful if we want to multiply 5 by itself seven times: 5 x 5 x 5 x 5 x 5 x 5 x 5 = 5⁷ (Five raised to the seventh power equals 78,125). The superscript 2 and the superscript 7 are called powers or exponents.