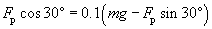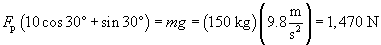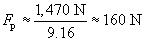In physics, work is the amount of energy required to perform a given task (such as moving an object from one point to another). We start by defining the scalar product of two vectors, which is an integral part of the definition of work, and then turn to defining and using the concept of work to solve problems.

Key Terms

o         Scalar product

o         Dot product

o         Work

Objectives

o         Recognize and use the scalar product of two vectors

o         Understand the concept of work in the context of physics

o         Calculate the work involved in moving objects from one location to another

Let's Begin!

More About Vectors

In some physics problems or situations, the ability to calculate the component of one vector in the direction of another is helpful. We saw some of this in our earlier study of vectors in relation to unit vectors: we are able to break down a vector such as 3x + 2y into its component parts: 3x (a vector of magnitude 3 in the x direction) and 2y (a vector of magnitude 2 in the y direction). But what if we want to calculate the component of some vector in the direction of another arbitrary vector? To this end, we define the scalar product (also called the dot product) of two vectors. (We call this the scalar product because the product is a scalar rather than a vector.) Given two vectors A = a₁x + a₂y and B = b₁x + b₂y, the scalar product A ? B is the following:

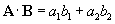
Note that A ? B = B ? A. We can factor out the magnitudes of A and B (A and B, respectively) and write the scalar product in terms of these magnitudes and the scalar product of two corresponding unit vectors, a and b, which are in the directions of A and B, respectively. (In other words, A = Aa and B = Bb.)

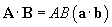
Now, let's consider these two unit vectors by way of the diagram below. Note that we have defined the angle between the vectors as ?.

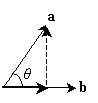
Note that the unit vector a is composed of a component vector in the direction of b and a component vector perpendicular to the direction of b. Using right triangle trigonometry, we see that the component of a in the direction of b is cos ? (the magnitude, or "length," of a is unity). We need to now prove that this result is the same as the scalar product of a and b. We'll draw two arbitrary unit vectors as shown below.

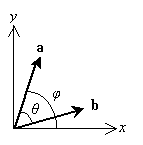
Notice that we have defined two angles: the angle ? between a and b, and ? between a and the x-axis. Let's write both a and b in terms of their component parts in the x and y directions (corresponding to the x and y unit vectors, respectively).

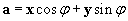
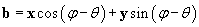
We'll calculate the scalar product of these two vectors as follows.

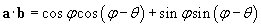
Let's use the properties of trigonometric functions (specifically, addition formulas) to simplify the result.

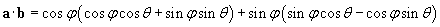
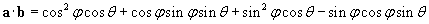
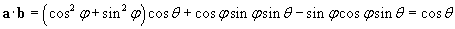
Thus, we have shown that the scalar product of two unit vectors that form an included angle ? is simply cos ?. We can therefore write the scalar product of two arbitrary vectors A and B as

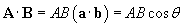
So, if we want to find the component of a vector A in the direction of another vector B, we can use the scalar product, but we must divide by the magnitude of B (which we represent as B), because this magnitude is not relevant. (Thus, the component of a vector A in the direction of B is the scalar product of A and b, following our current notation.) The diagram below illustrates this result.

Practice Problem: A projectile of mass 5 kilograms has a velocity 10x + 15y meters per second. What is the component of the projectile's momentum in the direction of 4x + 3y?

Solution: First, let's calculate the momentum p of the projectile.

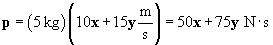
To find the component of the momentum in the direction of the vector 4x + 3y, we need to calculate the scalar product of p and the unit vector corresponding to 4x + 3y (we'll call this vector B). This unit vector, b, is the following.

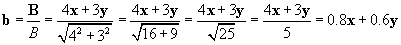
Now calculate the scalar product of p and b:

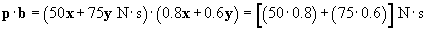
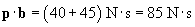
Thus, the component of the momentum in the direction of 4x + 3y is 85 newton seconds (the corresponding vector would be 85b newton seconds). This is compared with the magnitude of p, which is about 90.1 newton seconds.

Practice Problem: Show that the scalar product of two perpendicular vectors is always zero.

Solution: Consider any two vectors A and B where the angle between them is 90° (thus making them perpendicular). The formula for the scalar product of these vectors is the following, which was derived earlier.

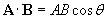
Let's insert the angle 90° into the formula.

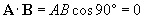
Thus, by virtue of the fact that cos 90° is zero, the scalar product of any two perpendicular vectors is zero.

Work

We typically think of work as something that involves an expenditure of effort--for instance, lifting a heavy box might be referred to as hard work. The concept of work in physics is similar; work in this context is defined as the product of the force applied to an object and the distance that the object is displaced (moved). For example, to lift the heavy box, one must apply an upward force to it over a certain distance; if the box needs to be lifted only a little bit, less work is done than if the box needs to be lifted high. Because both the force and the displacement have magnitude and direction, the work is not a simple product of two scalars. Instead, it is the product--specifically, the scalar product--of the two vectors. Thus, the work W done on an object is defined as follows, where d is the displacement vector.

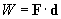
Notice that the units of work are newton meters (also called joules or J--a unit of energy). The scalar product above calculates the component of the force in the direction of the displacement (d_u, where d = dd_u) and then multiplies it by the total distance d of the displacement. (The formula above actually only applies to cases where F is constant; if F varies, then integral calculus is required to calculate work.)

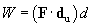
Let's consider what this result means. Let's say we want to pick up the box from our example illustration above and move it some distance before setting it down once again, as shown below. We define y as the unit vector in the upward direction and x as the unit vector in the rightward direction.

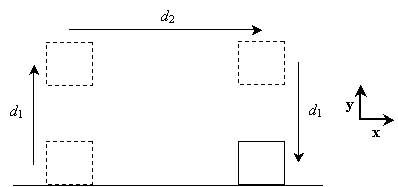
In each case, gravity pulls the box downward. When it is resting on the floor, the normal force balances gravity, resulting in no net force on the box and, therefore, no acceleration. In the first step (lifting the box to a height d₁ above the floor), the displacement vector is d₁y; in the second step, it is d₂x, and in the third step, it is –d₁y. All that is needed to move the object is sufficient force to counter the gravitational force. That is to say, according to the physics definition of work, only the first and third steps actually correspond to a non-zero value of the work done on the box. Let's see why. In the first step, the force applied to the object is upward and is equal to the gravitational force: mg, where g is equal to –gy (g = 9.8 meters per squared second) and m is the mass of the box. Thus, to lift the box, a force mgy is required over a displacement vector d₁y. Let's now calculate the work done on the box in this step.

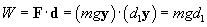
Thus, the total work done in lifting an object of mass m a distance of d₁ is mgd₁. (You might wonder about why we don't account for the initial acceleration of the box and the deceleration of the box at the end of the displacement. As it turns out, the acceleration and deceleration, although they do involve work, mathematically cancel because they correspond to forces that are equal in magnitude and opposite in direction.) Now, let's consider the horizontal movement of the box. We must still apply a force –mg to the box, since we must counter gravity to keep it suspended above the ground. The displacement vector, however, is x, which is perpendicular to the force vector. Thus, in this case, the work is the following:

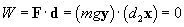
In other words, from the perspective of physics, no work is done on an object when it is moved in a direction perpendicular to the force applied to it. Finally, when we set the box back down, we are still applying a force –mg, but the displacement vector is –d₁y.

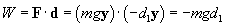
In other words, by lowering the box, we are doing "negative" work on it. Note that the total work done on the box in this process of moving it is zero:

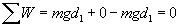
Practice Problem: A man lifts an awkward object of mass 50 kilograms by raising it from the floor in the direction of the vector x + 5y (assume x is horizontal and y is vertical--specifically, up). If he lifts the object 1 meter high, how much work has he done on it?

Solution: Let's draw a diagram illustrating the motion of the object.

To counter the force of gravity, the man must apply a force equal to mg in the upward direction. Although he may be moving the box in a diagonal direction, he is only applying a force in the vertical direction. Thus, F is mgy. The displacement vector has a horizontal and a vertical component, but we are only interested in the vertical component (because F has only a vertical component, the scalar product of F and d is the product of these vectors' vertical components). Because the box is raised by 1 meter, the relevant displacement vector is 1y m. We can now calculate the work done on the box.

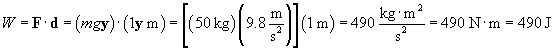
It is important to note that the path followed by the man lifting the object is not important; what matters is the initial and final heights of the object. If the man lifts the object 1 meter, he does 490 J of work on it, regardless of how he gets the box to this height.

Practice Problem: A woman is trying to slide a tall, heavy object of mass 150 kilograms across a rough floor. The floor produces a friction force equal to 0.1 times the normal force acting on the object. If the woman pushes in a direction that is 30 degrees above horizontal, how much work has she done if she moves the object 10 meters?

Solution: The normal force is the force applied by the floor to the object such that the object cannot be accelerated downward (through the floor). To calculate the friction force, F_f, we first need to calculate the normal force, N. The forces acting on the object as it is moved are shown below. The pushing force applied by the woman is F_p.

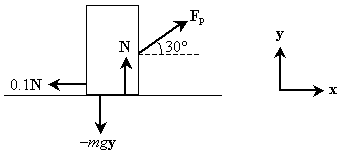
The displacement vector is 10x meters in the above case (the friction force, 0.1N, is in the direction opposite to the displacement of the object). The horizontal component of the pushing force, F_p, must be equal to the force of friction to move the object, but this force depends on N, where

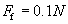
Then,

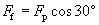
The total vertical force applied to the object, between gravity and the vertical component of the pushing force, is the same as the normal force. Thus,

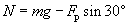
We can combine these last two expressions into the relationship between F_f and N and then solve for F_p.