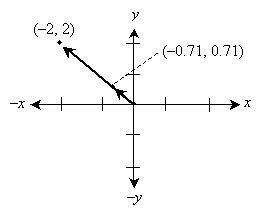Key Terms
o Frame of reference (reference frame)
o Scalar
o Vector
o Unit vector
Objectives
o Be able to define a set of coordinate axes and an origin for the purpose of locating objects and events
o Understand the difference between a scalar and a vector
o Know how to calculate the magnitude of a vector
o Recognize unit vectors
Let's Begin!
Introduction
Physics is the study of the characteristics and interactions of matter and energy in nature. One of the chief tools in physics is mathematics. As it turns out, the world is ordered such that we can apply mathematical rigor to our understanding of it. Thus, we will focus on how mathematical principles and techniques can be used in physics to solve various problems and to model physical phenomena. To be sure, the topic of math in physics could span numerous courses; as such, we will focus on some basic principles that rely on algebra, trigonometry, and geometry.
In this lesson, we will introduce a simple graphical (coordinate) method of representing the locations of objects and events. In addition, we will discuss scalars and vectors, which allow us to quantify physical phenomena that have either magnitude only or both magnitude and direction. These simple mathematical tools will provide us with a foundation on which we can build a system for analyzing motion, forces, energy, and other physical phenomena.
Locations of Objects and Events
Physical objects and events have a spatial extent or location. As a result, it is helpful to have an orderly way in which we can describe these characteristics mathematically. One way to describe the position (location) of, for instance, a particle is to use a set of mutually perpendicular axes, just as we might do when graphing a function y(x). Each axis corresponds to a direction (and its opposite), such as forward and backward or left and right. Each direction is mutually perpendicular with the other directions. (Obviously, if we are talking about three-dimensional space, which is largely how we perceive things and events around us, then we need only talk about three mutually perpendicular directions--up and down, left and right, and forward and backward, for instance.) In this course, we will deal primarily with objects and events in two dimensions for simplicity. The techniques and principles that we study, however, can easily (in most cases) be extended to three dimensions.
In addition to defining the mutually perpendicular dimensions for our system of identifying position in space, we also need to define a central point, or origin, that marks the spot from which we measure distances in each direction. A set of directions, or axes (marked as positive and negative x and y) and corresponding origin (point O) are shown below.
This system of locating an object or event might be as simple as a map where a city marks the origin, and the locations of other cities are noted as distances from the origin city in the directions north, south, east, or west. The choice of a set of directions and an origin is arbitrary as long as the axes (directions) are mutually perpendicular and span the proper space (the plane of interest, in the case of two dimensions--a map, for example, deals with directions in the plane of the Earth's surface). A set of axes and corresponding origin is also typically called a frame of reference (or reference frame) in the parlance of physics.
A location can be noted in two dimensions as a pair of coordinates of the form (x, y). Using standard algebraic graphing techniques, an object located at (�1, 5), for instance, could be shown as below.
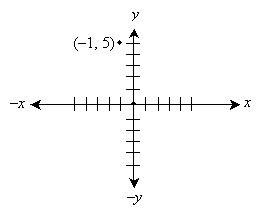
Vectors
In addition to identifying the location of a particular object or event, we may also want to quantify some other physical characteristic, such as temperature or velocity. In some cases, all we need is a number; for instance, we can talk about the temperature of an object by simply referring to a single number (and associated unit), such as 48 degrees Fahrenheit. This number is simply a magnitude that quantifies the physical characteristic--temperature, in the case of this example. In other cases, a number is not sufficient. The speed of the wind is helpful information, but it is not complete; in addition to a speed such as 20 miles per hour, wind also has a direction such as south or northeast. We therefore need more than just a simple number (called a scalar) to quantify characteristics such as velocity or force: we need to quantify direction also. For this purpose, we define a vector, which is a quantity with both a magnitude and a direction.
Graphically, we can show a direction using an arrow; we can also show a magnitude by the length of the arrow. An example of a vector with length of four units and directed in the positive y direction is shown below. Note that a vector has magnitude and direction but not location. For instance, imagine a wind of 40 miles per hour in the eastward direction. Whether such a wind blows in one place or another, it still has the same magnitude and direction. Likewise, a vector with a given magnitude and direction is the same regardless of its location. As a result, each vector shown in the graph below is identical because each has the same magnitude (four units) and direction (positive y).
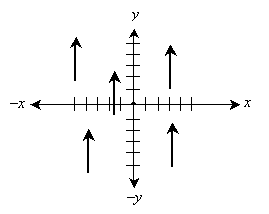
The graphical form of a vector has two essential parts: the head (the endpoint corresponding to the arrow) and the tail (the endpoint opposite the head).

We would like to be able to assign a vector a simpler numerical designation that does not require us to specify magnitude and direction separately. Because a vector has no particular location, we can place the tail on the origin of our graph; thus, the tail is located at point (0, 0). Thus, only the head has a location whose coordinates are non-zero. To perform this relocation of the vector representation, we can simply subtract the tail coordinates from both the head coordinates and tail coordinates. This translates the vector such that the tail is at (0, 0), or the origin. We can therefore identify a vector using a simple coordinate pair: for instance, (0, 4) in the case of the vector shown in the above graph.
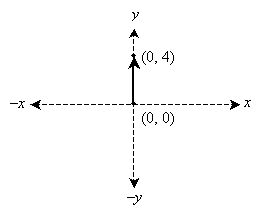
Since this notation for a vector is identical to that for a point, it is important to differentiate between points and vectors. Symbolically, we can identify a particular symbol as a vector using boldface instead of standard font--for instance, we might label a point as P, but a vector we would label V. Because our method of identifying a vector V using (x, y) format is the same as we might use to identify a line segment starting at the origin and ending at the point (x, y), we can use the distance formula to find the magnitude of V. We can call this magnitude V or, using the "absolute value" notation, 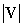 .
.
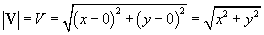
For our example vector (0, 4) above, the magnitude would be the following.
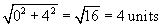
Practice Problem: Draw a graph of the vector (�3, 4) and find its magnitude.
Solution:
To graph the vector, start by drawing a set of axes, then plot the point (�3, 4). Draw an arrow from the origin to this point, as shown below.
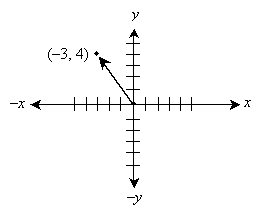
To calculate the magnitude (length) of this vector, use the distance formula.
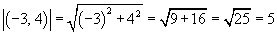
Thus, the vector has a length of 5 units.
Practice Problem:
A vector has its head at (1, 2) and its tail at (4, �1). Find the magnitude of this vector.
Solution: We can view this problem in one of two ways. One approach is to note that a vector has no particular location, so we can go ahead and apply the distance formula to the vector using the coordinates given in the problem statement. A second approach is to move (translate) the vector so that its tail is at the origin; we can then apply the distance formula at that point. Let's show that these two approaches yield the same result. First, we'll apply the distance formula to the vector using the given coordinates. We'll call the vector V.
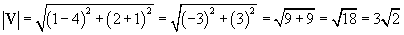
Now, let's translate the vector as shown below. To do this, we move the tail (and, likewise, the head) down two units and left one unit. (Another way of looking at this is that we have simply subtracted the tail coordinates from the corresponding head coordinates.)
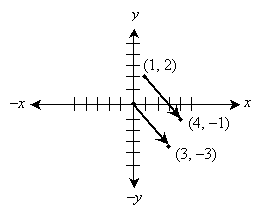
Now, let's calculate the magnitude of the vector with its tail on the origin.
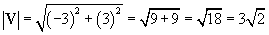
Thus, both approaches yield the same result.
We can also (in some sense) determine the direction of a vector, just as we did above for the magnitude. In this case, however, we still require (x, y) coordinate format for the direction. Note that if we divide a vector V by its magnitude 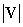 , we end up with a new vector U that is in the same direction as V but that has a magnitude of unity. To multiply or divide a vector of the form (x, y) by a scalar c, simply perform the operation on each individual coordinate: for instance, c(x, y) = (cx, cy) and
, we end up with a new vector U that is in the same direction as V but that has a magnitude of unity. To multiply or divide a vector of the form (x, y) by a scalar c, simply perform the operation on each individual coordinate: for instance, c(x, y) = (cx, cy) and 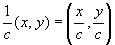 .
.
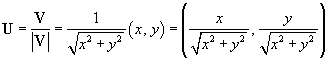
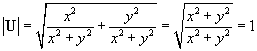
The vectors U and V have the same direction because their x values have the same constant of proportionality as do their y values. This means that they have the same slope, if we consider this situation from the perspective of "rise over run" (a simple way of understanding slope). Since U has a magnitude of unity, we call it a unit vector. Note that, on the basis of the expressions above, any vector V is the product of a unit vector U and a scalar magnitude 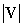 (or V):
(or V):
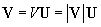
Practice Problem: Find the magnitude of a vector V = (�2, 2). Also find a unit vector in the direction of V.
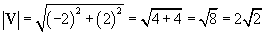
The corresponding unit vector U is simply V divided by the magnitude we calculated above.
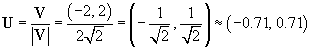
Let's plot the vectors U and V to show that they are parallel (because both have their tails on the origin, these vectors overlap).