o         Acoustic waves

o         Traveling waves

o         Wavelength

o         Compressibility

o         Bulk modulus

o         Density

Objectives

o         Develop a mathematical expression for traveling waves

o         Determine the relationship between wave speed, frequency, and wavelength

o         Relate sound waves to pressure variation in a medium

o         Be able to calculate wave speed from the bulk modulus and density of a medium (and vice versa)

Let's Begin!

In this article, we look a little deeper into the properties of waves and then apply those properties to the study of acoustic waves, or sound waves. An acoustic wave is a type of mechanical wave where pressure variation propagates through a material. For example, the speaker of a radio has a membrane that responds to an electrical signal by moving back and forth. This movement causes a brief change in the air pressure near the speaker; but this region of high pressure has a tendency to expand, equalizing the pressure with the surroundings. As it expands, it causes pressure changes around it, and so on, causing these pressure changes to travel outward, eventually intercepting the ear. Inside the ear, a biological membrane is moved back and forth by these pressure changes, creating a signal that is interpreted by the brain as sound. (You can also feel very loud sounds throughout your body!) This is one example of an acoustic wave. Before going into greater depth regarding acoustic waves, we consider a few more details about waves in general.

More About Waves

We can now consider traveling waves. An example of a traveling wave is a wave in the ocean; the wave has the appearance of movement in a particular direction and at a particular speed. Let's consider our expression for a sine wave once more, but let's more carefully specify the phase ? of the function.

Recall that different values of ? result in a displacement of the wave in one direction or another. Imagine a wave moving in the x direction. If we take a series of measurements in time at one location, say x = 0 meters, and at another location, say x = 1 meter, we find that the measurements do not "line up"; this is to say, the value measured at x = 0 for some time t are not necessarily the same as those measured at x = 1 at the same time. This is simply because the wave is traveling: the portion measured at x = 0 requires some time to reach x = 1 (assuming the wave is traveling in the positive x direction). This delay is illustrated in the diagram below, where a traveling sine wave is plotted as a function of distance at two different times.

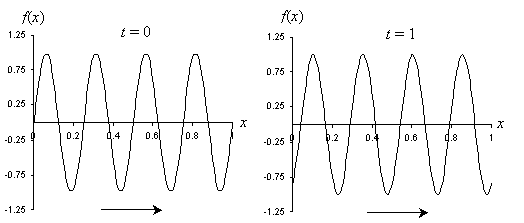
Obviously, this looks like a phase change of the wave. But how can we incorporate this into our expression for the sine function? Note that the sine function in terms of x is identical in shape to the sine function in terms of t; thus, we'll simply write the phase ? of A sin(?t + ?) in a form similar to that of the time portion. Let ? be –kx, where k is analogous to ?. The sine function for a traveling wave is then in terms of x and t.

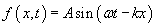
(This function is often written as Asin(kx – ?t) instead--this, however, is simply the same function with an added phase shift of ?. In other words, Asin(?t – kx + ?) = Asin(kx – ?t). We will use the form above, however, in accordance with the way we have developed our understanding of waves. The same principles apply in either case, though.)

If we went through an analysis, we would find that 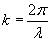, where ? is the wavelength of the sine wave. (If ? is in units of meters, then k is in units of inverse meters.) The wavelength is similar to the period; the period of the wave is the "wavelength" in time, and the wavelength is the "period" in space.

Now, consider that the period (time) between successive peaks is T (equal to 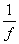) and that the wavelength (distance) between those peaks is ?; the speed v of the traveling wave is simply the wavelength divided by the period.

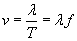
Practice Problem: A scientist taking measurements of water waves near a beach chooses two piles of a pier, which are 10 meters apart, to help her make her measurements. She watches one wave and starts a timer when the peak hits the first pile; she stops the timer when that same peak hits the second pile. The timer indicates that the wave peak took 14 seconds to reach the second pile from the first pile. The scientist also uses the timer while watching the waves at a single pile to measure the period. If the wave period is 4 seconds, what is the wavelength of the waves?

Solution: Earlier, we learned that the velocity, wavelength, and period of a wave are related by the following expression.

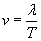
The problem statement tells us that the waves travel 10 meters (the distance between the two piles) in 14 seconds. From this information, we can calculate the wave speed v.

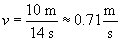
Now, using the formula above and the wave period of 4 seconds, we can calculate the wavelength (the spatial distance between successive peaks or troughs) as follows.

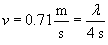
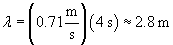
Thus, the wavelength is approximately 2.8 meters. Note that the scientist needed to only know the distance between the piles; she would then be able to derive the wavelength through just timing measurements of the waves.

Acoustic Waves

Now that we have something of a mathematical foundation for understanding waves in general, we can now turn to a specific type of wave: acoustic waves. Let's consider more carefully the case of a speaker. Although we will not undertake an exhaustive mathematical derivation of the details of this or other similar cases, we can show conceptually how the math relates to the physical phenomenon. Below is a diagram that shows the speaker; when the speaker's membrane is displaced outward by the signal, it causes an increase in the nearby air pressure, which then travels outward. Likewise, when the membrane is displaced inward, it causes a decrease in the nearby air pressure. If the speaker is fed a sinusoidal electrical signal, we can expect the motion of the membrane to be sinusoidal, resulting in an outward-traveling sinusoidal pressure wave. This wave is shown below, where the solid lines indicate a wave peak and the dashed lines indicate a wave trough.

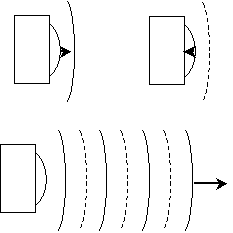
Air has a certain "ambient" pressure; thus, these wave peaks and troughs represent variations above or below that ambient pressure. If we call this pressure variation ?p, where a positive value represents compression (increased pressure) and a negative value represents expansion (decreased pressure), then we can write an expression for this pressure (sound) wave as follows. We assume here that the wave is traveling in the positive x direction. Pressure has SI units of newtons per square meter (you may also have heard of pressure being measured in pounds per square inch, for instance).

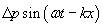
The speed of a sound wave in a medium (such as air) depends on the properties of that medium. By way of analogy, imagine you are holding the end of a rope, with the other end tied to a large tree or other steady object. If you pull the rope taut and then tug at a portion of the rope briefly, you will see a wave travel out to the tree and then back. If you pull the rope so that it is tighter, the wave will travel faster. In this latter case, more effort is also required to tug at the rope so that a wave is created. Media through which sound travels act in a similar manner: they have a certain compressibility, which (as the name indicates) is a measure of how easily the material can be compressed. The reciprocal of compressibility is the so-called bulk modulus, B. A high bulk modulus (which corresponds to a small compressibility) indicates that the medium's volume changes little when pressure on it is increased or decreased (rock, for instance, has a high bulk modulus). Concomitantly, a small bulk modulus (high compressibility) means that the medium's volume changes greatly when pressure on it is increased or decreased. The speed of a sound wave increases as the medium's bulk modulus increases. Another factor in the speed of sound is the density of the material composing the medium; a higher density results in a slower speed of sound, and a lower density results in a higher speed of sound. The relationship between the wave speed v and the material's bulk modulus B and density ? is the following.

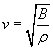
The bulk modulus has SI units of newtons per square meter (the same as pressure--this unit is also known as a pascal, or Pa), and density has units of kilograms per cubic meter. You can easily show that, using the above formula, these units produce meters per second for the velocity.

Practice Problem: A sound source is lowered into a body of water having a density of about 1,000 kilograms per cubic meter. The source produces waves at a frequency of 100 hertz. If the wavelength of the sound waves is about 14.8 meters, what is the bulk modulus of the water?

Solution: This problem requires that we apply much of what we have learned about the properties of waves and the relationship of wave speed to the properties of the medium. First, let's calculate the wave speed in water using the given wavelength and frequency.

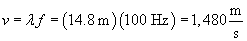
We are told that the water has a density of about 1,000 kilograms per cubic meter; using the velocity of the wave and this density, we can calculate the water's bulk modulus.

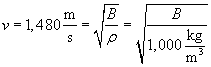
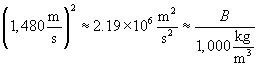
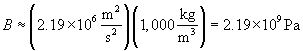
Thus, the bulk modulus of the water is about 2.2 billion pascals.

Practice Problem: A certain sound wave in air can be described by the expression
400 sin(6,300t - 18.3x) pascals, where t is measured in seconds and x in meters. What is the speed of sound in air?

Solution: The general expression we used for sound waves is
?p sin(?t - kx), where

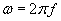
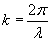
From the given expression, we can calculate the frequency (f) and wavelength (?) of the wave. Note that the units of t are seconds, meaning that f is in hertz. Likewise, because x is measured in meters, ? is also measured in meters.

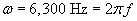
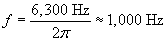
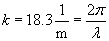
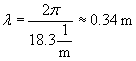
We can now calculate the speed of sound in air, v.

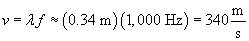
Thus, from the given expression, we find that the speed of sound in air is about 340 meters per second.