Key Terms
o Deductive reasoning
o Deduction
o Premise
o Conditional statement
o If-then statement
o Antecedent
o Consequent
o Proof by contradiction
o Two-column proof
Objectives
o Know how to derive conclusions from premises using basic deduction
o Recognize a two-column proof
o Recognize the importance of units in geometric measurement
o Understand how arbitrary units are used in measurement
Before we begin to take a more in-depth look at geometry proper, it behooves us to first review some basic rules of deductive and mathematical reasoning that will aid our analyses. The methods of deductive and mathematical reasoning can also be of great benefit even beyond geometry and mathematics. In addition, we can consider some aspects of measurement as they apply to geometry.
Deductive Reasoning in Geometry
Deductive reasoning (or deduction) is the process of deriving logically necessary conclusions from a set of premises, which are simply statements or facts. Another way of stating this definition is that a conclusion reached through the process of deduction is necessarily true if the premises are true. Premises are often either simple statements, such as "all squares are rhombuses" or "a rectangle has four sides," or slightly more involved conditional statements (also known as if-then statements), such as "if a polygon has three sides, then it is a triangle." We can look at if-then statements in a general sense by considering a basic form: if x, then y. In this format, x is the antecedent (or premise), and y is the consequent (or conclusion). Assuming the conditional statement is true, then it logically follows that if x is true, y must also be true. If x is false, however, then we cannot draw any conclusions about y. Let's consider these properties by way of some practice problems.
Practice Problem: What conclusions, if any, can be drawn from the following statements?
A: Figure x is a rhombus.
B: If a figure is a rhombus, then it has four sides.
Solution: We are given premises A and B, where A is a simple factual statement and B is a conditional statement. The conditional statement tells us that if a figure is a rhombus, then it has four sides. Premise A tells us that figure x is a rhombus. As a result, because the antecedent ("a figure--x in this case--is a rhombus") is true, the consequent ("x has four sides") must also be true. We can therefore conclude that figure x has four sides.
Practice Problem: Determine whether any conclusions can be drawn from the following statements.
A: Figure x is an ellipse.
B: If a figure is a circle, then its diameter is proportional to its circumference.
Solution: Note that figure x is identified in premise A as an ellipse; although this does not rule out x being a circle, we cannot be sure from the given information. As a result, the antecedent of premise B may or may not be true in the case of figure x. We therefore cannot draw any conclusions on the basis of these premises.
Definitions in geometry can be thought of as conditional statements. For instance, we might define a rhombus as follows: "A rhombus is a quadrilateral with all four sides of equal length." We can recast this statement as follows: "If all four sides of a quadrilateral are of equal length, then it is a rhombus." Note that the force of the conditional statement is the same as that of the definition, but it provides us with a tool for drawing conclusions using deduction.
Practice Problem: A quadrilateral containing only right angles is a rectangle. Quadrilateral P contains only right angles. What conclusions (if any) can be drawn about P?
Solution: Let's write the premises in the problem as follows:
A: If a quadrilateral contains only right angles, then it is a rectangle.
B: Quadrilateral P contains only right angles.
Clearly, then, quadrilateral P is a rectangle.
Sometimes, we do not have enough information to perform a simple series of direct deductive steps to reach our desired conclusion. In such cases, proof by contradiction is another potential approach. Let's assume we want to prove some statement, such as "figure D is a square." Although a direct proof may not possible (depending on what information we are provided with), a proof by contradiction may be possible. We perform a proof by contradiction by assuming the opposite of what we want to prove-in this case, "figure D is not a square." We would then apply our standard deductive tools until we reach a contradiction (for instance, we conclude that a true premise is false). At this point, we know that our assumption must be false because it is not logically consistent. The following practice problem illustrates a proof by contradiction.
Practice Problem: For a quadrilateral U, no two sides are parallel. If a quadrilateral is a parallelogram, then it has two pairs of parallel sides. Prove that U is not a parallelogram.
Solution: There is no direct way to prove that U is not a parallelogram, so let's assume the opposite: assume that U is a parallelogram. We can then conclude from the conditional statement given in the problem that U has two pairs of parallel sides. This conclusion, however, contradicts the statement in the problem that U has no parallel sides. Thus, we must reject our assumption, thereby proving that U is not a parallelogram.
These few basic facts provide an acceptable foundation for reasoning in the context of geometry. Much of the reasoning that we will do involves the use of definitions and basic facts, along with conditional statements, to derive conclusions about geometric figures. A formal method of displaying the process of reasoning in geometry is the two-column proof, which includes premises and derived conclusions on the left-hand side and the reasoning for each step on the right-hand side. The ability to recognize two-column proofs is beneficial. Let's consider a short example. Let's say we are analyzing the figure below (not necessarily drawn to scale).
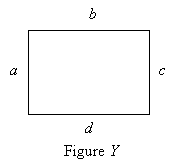
Assume we are told that a = b = c = d, and we know that a rhombus is defined as a quadrilateral with four sides of equal length. Our given task is to prove that the figure in the diagram above is a rhombus. A two-column proof in this case might look like the following.
1. a = b = c = d Given
2. If a quadrilateral has four Definition of a rhombus
sides of equal length, then it is a rhombus.
3. Figure Y is a quadrilateral Figure in diagram has four sides
4. Figure Y is a rhombus Statements 1, 2, and 3
Measurement in Geometry
Geometry sometimes involves measurements of the characteristics of a figure. For instance, we may be interested in determining the length of a line segment. Mostly for our purposes, we do not use units to describe measurements-instead, we simply use numbers. In real life, however, a number isn't always helpful. If a construction worker were to say that a steel beam was 78 long, no one would be able to figure out how long the beam is. If the construction worker said (or otherwise implied) 78 inches, or 78 meters, or 78 with some other unit, then we would be able to identify the length of the beam. Thus, units are a critical part of geometry, even though they may be omitted when we are analyzing figures that do not necessarily correspond to any particular object in the real world.
Units of measurement are based on arbitrary standards. For instance, a foot is simply the length of some object that people have agreed to use as a standard for length. Thus, when performing a measurement, the characteristic being measured is compared to the arbitrary standard. If we called the length of a certain bar a foot, then we could measure the length of a line segment by determining how many feet it is. In the example diagram below, the line segment is shown to be four feet long.
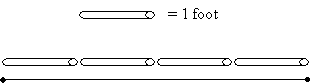
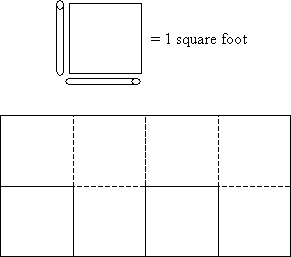
In addition to lengths, we can also measure areas. Units of area are defined using square feet, square meters, or some other square length unit. Such a unit is simply a square whose sides have a length of one foot, one meter, or one of whatever unit is being used for the measurement. The area of a figure is simply the number of these square units that we can fit inside the bounds of that figure. (To be sure, as with length, we may need to use portions of a unit to fill in small regions. These portions are simply fractional values of the unit, however.) The diagram below shows a rectangle that is eight square feet in area.
Volume, likewise, involves cubic units, as shown below. We might imagine a three-dimensional figure being hollow, and our cubic unit like a cup that we can fill with water. We measure the volume, according to this heuristic approach, by filling the unit with water and pouring it into the figure until the figure is filled. In the example below, the cylinder might be (for instance) 2.5 cubic feet, or two and one-half of the cubes filled with water and poured into the cylinder. A cubic foot is the volume of a cube whose sides all have a length of one foot.
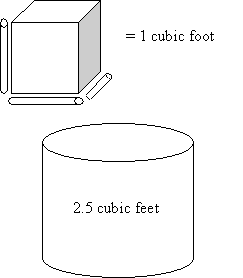
Another important geometric parameter that we can measure is angle. Armed with an understanding of geometric reasoning and the nature of measurements in geometry, we can begin to analyze figures and the relationships between them.
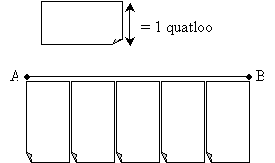
Practice Problem: Using the arbitrarily defined length shown, determine the length of the line segment ![]() .
.
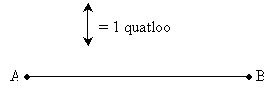
Solution: One approach is to take any available object (a pencil or a scrap of paper, for instance), mark off (with a pencil or just your finger) the length of a "quatloo," then determine how many quatloos are needed to span the length of the line segment. As shown below, the result is about 5 quatloos. (Obviously, the term "quatloo" has been invented for this situation-nevertheless, we are able to do this legitimately, since units are based on arbitrary standards!)