Key Terms
o Composite figure
Obviously, not all geometric figures are simple polygons or circles. In many instances, a geometric figure is composed of a number of different figures, such as triangles, quadrilaterals, circles, and so on. Such a figure is called a composite figure. Although such figures have arbitrary shapes, meaning that we cannot derive simple formulas for their areas, perimeters, or other features, we can often use what we have learned about simpler geometric figures to calculate these quantities for more complex composite figures. The key to solving such problems is to divide the composite figure into a set of simpler figures whose characteristics we know how to derive or calculate. Therefore, we'll focus on applying what we have learned about various simple geometric figures to analyze composite figures. A number of practice problems illustrate the basic approach.
Composite Figures
As mentioned above, composite figures are best analyzed by dividing them into smaller figures whose characteristics we can readily determine. Of critical importance is recalling the characteristics of simpler figures, such as squares and circles. Let's consider the following figure, for instance, whose area and perimeter we want to calculate.
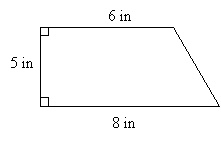

The figure is a trapezoid, but assume for the moment that you don't recall the formula for the area of a trapezoid. Recall that a rectangle contains four right angles; thus, if we divide the figure with a vertical line as shown below, we create a rectangle and a right triangle.
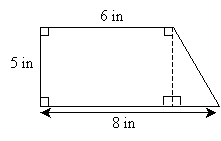

Now, because opposite sides of a rectangle are equal, we can fill in some gaps in what we know about the figure. By applying simple arithmetic, we find that the base of the triangle is 2 inches.
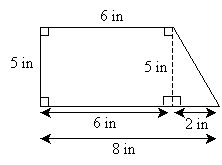

Finally, let's apply the Pythagorean theorem to find the length of the only remaining unknown side, x.
![]()
![]()
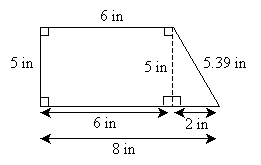

We now have everything we need to calculate the area A and perimeter P of this figure.
![]()
![]()
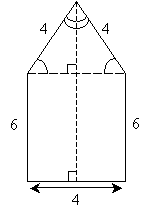
Practice Problem: Find the area and perimeter of the figure below.
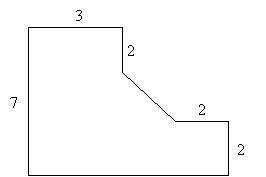 77
77
7
Solution: By inspection we can see that this figure is composed of two rectangles and a triangle. Let's divide the figure accordingly and, using the properties of rectangles, fill in as many "blanks" as possible.


This gives us enough information to find the area of the figure, but we must also find the hypotenuse h of the triangle if we are to calculate the perimeter. Again, we can use the Pythagorean theorem.
![]()
![]()
The area A (using the formulas for rectangles and triangles) and perimeter P of the figure are then the following.
![]()
![]()
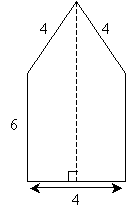
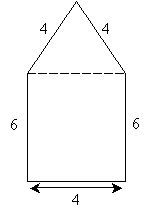
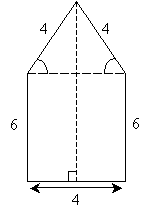
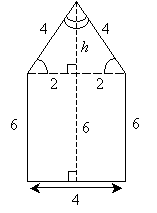
Thus, the length of the (vertical) dashed line segment is 9.46 units.
Figures may also include circles or portions thereof. In such cases, you may need to calculate the area of a sector or the length of an arc when determining the area or perimeter (respectively) of the figure. The same principles used above, however, apply in these cases as well. The following practice problems give you the opportunity to test your skills in this area.
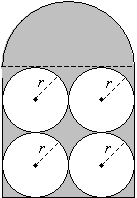
Solution: All we are given for this figure is that each of the white circles has a radius of r. Thus, we know that the white area is four times the area of one of the white circles.
![]()
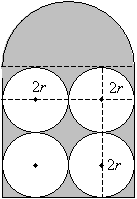
The area of the square is thus 16r2. In addition, the radius of the semicircle is 2r, so that its area is the following.
![]()
We can now combine all this information to calculate the area of the shaded region.
![]()
Practice Problem: What is the diameter of the circle containing the rectangle shown below?
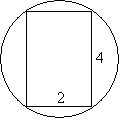

Solution: This problem has some difficult aspects, but we can solve it. The most important point in this case is that the vertices of the rectangle lie on the circle; thus, we can draw radii from the circle's center to each corner of the rectangle.
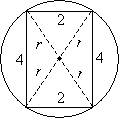

What we have done here is divide the rectangle into four triangles. By the SSS condition, we see that the figure contains two pairs of congruent triangles: the two triangles with sides r, r, and4, and the two triangles with sides r, r, and 2. What we need to do now is show that two radii actually form a diagonal of the rectangle-this condition is not a given. To do so, let's recall what we know about parallel lines. Two parallel lines cut by a transversal line will have congruent corresponding angles. Because the pairs of triangles in the diagram are congruent and isosceles, we can identify the following congruent angles.
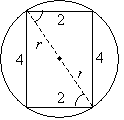

We know that the sides of length 2 are parallel by virtue of the properties of a rectangle. Because the radii both form congruent angles as shown above, they lie along the same transversal line segment. Thus, these two radii form a diameter of the circle. (In other words, the two radii form a straight angle at the center of the circle.) The diagonal of the rectangle is thus 2r. We can now use the Pythagorean theorem to find the radius.
![]()
![]()
![]()
![]()
We thus have determined the radius of the rectangle to be approximately 2.24 units.
























