Key Terms
o Exponential function
o Logarithmic function
o Natural logarithmic function
Objectives
o Know the basic properties of exponential and logarithmic functions
o Learn how to apply these functions to solving problems, including word problems
Exponential Functions
We should already know that certain expressions involve a variable raised to a power other than 1. What if we instead raise a constant (a number) to a variable power? The result is an exponential function, which is expressed in general form below.
f(x) = abx
The function f(x) has a constant coefficient a and a constant base b raised to the power of x, which is a variable. Two common bases that you may encounter in problems and in real life applications are 10 and the number e (e ≈ 2.7183). As with polynomials of degree 2 or greater, exponential functions are nonlinear (assuming, of course, the base b is not equal to zero). Let's take a look at the plot of an exponential function using a base of e. (Note that calculating the exponent--or even logarithm--of a number is generally very difficult to do; calculators are required more often than not.)
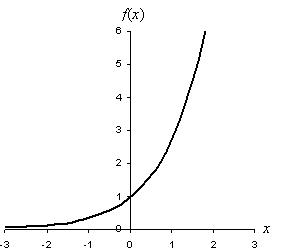

Notice that the graph of the function steadily increases in slope as x increases and that it approaches zero as x gets smaller. The range of the function is thus f(x) > 0.
Before we continue, let's review some of the basic properties of exponents in the context of algebra. Remember, a letter or other symbol in algebra is simply an unknown or unspecified number.
![]()
![]()
![]()
![]()
![]()
![]()
Also, we can relate exponential functions to the use of radicals:
![]()
So, the square root can be represented several ways (the second representation below is not used since it is generally understood that the radical alone means square root):
![]()
Practice Problem: Simplify the expression 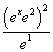 and sketch the graph the result.
and sketch the graph the result.
Solution: We can apply our rules of exponential functions to this expression as follows.
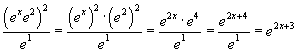
![]()
Now let's sketch a graph the function.
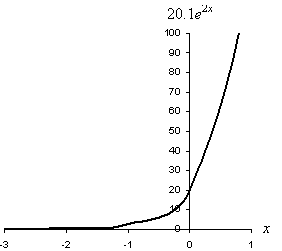

Note the scale of the function: to see its behavior, we must look at a much larger range on the vertical axis. This shows how seemingly tame exponential functions can expand to extremely large values very quickly.
Logarithmic Functions
A logarithm is the inverse function of an exponential. That is, given f(x) = ex and g(x) = ln x (where "ln" indicates natural logarithm, as we will discuss briefly), then
f(g(x)) = eln x = x
g(f(x)) = ln (ex) = x
Generally, we express a logarithmic function as loga x, where a is the base of the logarithm. When the base a is equal to e, then we have a special logarithmic function that we call a natural logarithmic function, or simply a natural logarithm. We express this function as ln x. The following expression shows the relationship between logarithms and exponentials:
loga (ax) = x
The graph of a natural logarithmic function f(x) = ln x is shown below.
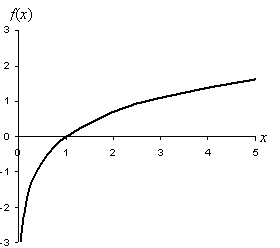

Notice that the domain of the logarithm is limited to x > 0, since there are no real values defined for the logarithm when x is zero or less than zero. (Consider, for instance, the inverse function: if y = ln –a, then ey = –a, but there is no real value of y that could make an exponential negative.)
The following are some properties of logarithms in the context of algebra. These logarithms are, for the most part, expressed using ln instead of log, but the same properties apply in both cases.
ln x + ln y = ln (xy) ln xy = yln x
ln x - ln y = ln![]()
![]()
The one property expressed in terms of log functions is the so-called change of base formula. This expression allows you to take a logarithm in one base and convert it to an equivalent logarithm using a different base.
Practice Problem: Simplify the expression ln x3 + 3(ln 2 - ln 2x).
Solution: We can apply our rules for logarithms to simplify the expression as follows.
ln x3 + 3(ln 2 – ln 2x) = 3ln x + 3ln 2 – 3ln 2x
= 3(ln x – ln 2x + ln 2)
= 3ln ![]()
= 3ln 1 = 0
Thus, the expression is equal to zero (regardless of the value of x).
Applications of Exponential and Logarithmic Functions
We have now seen the basic algebraic aspects of exponential and logarithmic functions, but how can we use these functions? Let's take a look at some practice examples.
Practice Problem: Solve for x: 4πx = e.
Solution: If we rely solely on what we know about polynomials and linear functions in algebra, we will not have the tools we need to solve this problem. What if we apply our rules regarding logarithms, however? We see that this equation involves an exponential function; let's take the inverse of that exponential and see what happens.
4πx = e
ln(4πx) = ln e = 1
ln(4πx) = ln 4 + ln πx = ln 4 + x ln π = 1
x ln π = 1 - ln 4
x = ![]()
We can test this result by substituting it back into the original expression:
4π -0.337 ≈ 2.720 ≈ e
The result checks out. (To be more certain, calculate x to additional decimal places-the more accurate the x value, the closer 4πx will be to e.)
Practice Problem: The amplitude (maximum displacement) of a block attached to a spring decreases exponentially with time according to the function e–rt (where t is time in seconds). If the block's amplitude is half its initial value after 5 seconds, how long before it reaches 10% of its initial amplitude?
Solution: Let's take it one step at a time. First, note that an object on a spring (once displaced) will oscillate back and forth regularly, but it will eventually come to a stop. Keeping this context in mind, we want to find the time at which the amplitude of the oscillation reaches 10% of its maximum (the maximum amplitude of the object--block in this case--is when it is first displaced). The function that expresses the (relative) amplitude of the block is e–rt.
We are told that the amplitude is half its value when t is 5 seconds. We can use this fact to find the value of r.
![]()
Take the natural logarithm of both sides and solve for r:
![]()
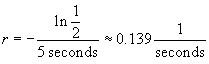
Notice that r has units of inverse seconds (also known as Hertz), which is a rate. Now, let's use this to find t when the amplitude is 10%, or 0.1.
![]()
![]()
![]()
![]()
Thus, it takes about 16.6 seconds for the amplitude of the block on a spring to decrease to 10%.
























