Key Terms

o Polygon

o n-gon

o Perimeter

o Equilateral

o Equiangular

o Regular polygon

Objectives

o Recognize polygons and their associated nomenclature

o Calculate the perimeter of a polygon

o Identify the special characteristics of regular polygons

Triangles and quadrilaterals are actually part of a larger class of figures called polygons, which are closed n-sided figures. (A polygon with n sides is sometimes called an n-gon.) Several examples of polygons are shown below.

Obviously, the more complex polygons (such as the two bottom figures above) have no apparent simple formulas for calculating such properties as the enclosed area or the length of diagonal line segment. As a result, we will limit our discussion to mainly simple convex polygons. (The terms simple, complex, concave, and convex have the same definitions for polygons as they do for quadrilaterals.) Note, however, that complex and concave polygons can be subdivided into more manageable polygons (such as triangles) for the purposes of calculating area or other parameters.

Polygon Nomenclature

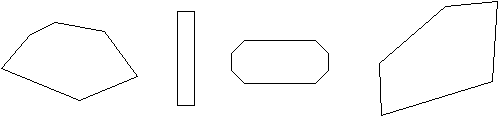
Polygons have a moderately systematic nomenclature, and understanding this nomenclature can be helpful. For instance, you may have heard of the Pentagon (the home of the United States Department of Defense), which is a five-sided building, or you may have heard other terms such as octagon or hexagon. Again, these names are largely chosen in a systematic fashion. The common names of polygons with five to ten sides are listed below; note that the terms triangle and quadrilateral do not follow this nomenclature.

pentagon five-sided polygon

hexagon six-sided polygon

heptagon seven-sided polygon

octagon eight-sided polygon

nonagon nine-sided polygon

decagon ten-sided polygon

More complicated prefixes apply to polygons with more than 10 sides, but for the sake of simplicity, we will simply refer to these using the n-gon terminology (for instance, we will use 11-gon to refer to an 11-sided polygon).

Interested in learning more? Why not take an online Geometry course?

Practice Problem: Identify appropriate names for each polygon below.

Solution: In each case, simply count the number of sides and follow the nomenclature described above. Be careful to note that we use the terms triangle and quadrilateral for three- and four-sided polygons, respectively.

Properties of Simple Convex Polygons

An arbitrary n-gon has n sides, n vertices, and n interior angles. For triangles and quadrilaterals, we were able to determine how many degrees are included in all the interior angles. We can do the same for arbitrary n-gons using similar reasoning. Let's first consider a specific example-a pentagon.

Because we already know how many degrees are in an arbitrary triangle or quadrilateral, our best approach to determining how many degrees are in a pentagon is to divide the pentagon into figures we already know. Let's divide the figure above into three triangles, as shown below.

Note that the subdivision used above is not the only possibility-other subdivisions are also acceptable. The pentagon thus contains three triangles, each of which has interior angles that sum to 180°. Because these interior angles also span all the interior angles of the pentagon (that is, if you add together all the interior angles of the triangles, the result is the same as all the interior angles of the pentagon), the total number of degrees in the pentagon should be three times 180°, or 540°. Let's take a look at a hexagon.

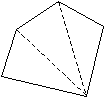
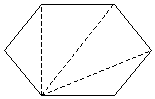
A hexagon can thus be divided into four triangles, for a total of 720°. We can see a pattern beginning to develop: with each additional side, a polygon gains 180° in its sum of interior angles. Let's derive a general formula for the number of degrees in an n-gon. First, we know that an n-gon has n sides and n vertices. As we have done above, we divide the n-gon into triangles by picking one vertex and then drawing dividing segments to each non-adjacent vertex. So, if we pick one vertex of an n-gon, we are left with n – 1 remaining vertices. Two of these vertices are adjacent to the chosen vertex, leaving us with n – 3 vertices to which we will draw dividing segments. Also notice from the above examples that if we draw m dividing segments in a polygon, we end up with m + 1 triangles. Thus, drawing n – 3 dividing segments yields (n – 3) + 1, or n – 2, triangles. Each triangle has 180°, so the formula for the number of degrees in an n-gon is

 

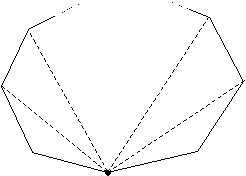
In addition, we may also be interested in determining the perimeter of a polygon, which is the total length of all the sides in the figure. Obviously, then, we can calculate the perimeter by adding the lengths of all the sides. For instance, a square with sides of length 2 meters has four sides of 2 meters each, for a perimeter of 8 meters.

Practice Problem: How many degrees are in a decagon?

Solution: A decagon is a polygon with 10 sides (in other words, an n-gon with n = 10). Thus, we can calculate the number of degrees in the figure using our formula from earlier.

 

Thus, the sum of the measures of the interior angles of a decagon is 1,440°. If you ever have trouble recalling the formula, draw an arbitrary decagon (make it as simple as possible!) and divide it into triangles. Then, multiply the number of triangles (eight in this case) by 180°. This approach, although slightly more involved, is equally as valid as using the formula.

Regular n-gons

If all of the sides of a polygon are congruent (that is, the polygon is equilateral) and all the angles are congruent (that is, the polygon is equiangular), then it is called a regular polygon. Because all the angles of a regular n-gon are congruent, the measure of each of those angles is simply the total number of degrees in the n-gon divided by the total number of angles (n).

Measure of any angle in a regular n-gon =

For an n-gon with sides of length x, the perimeter is simply nx (since the figure has n sides of length x). Calculating the area of a regular n-gon can be done, but deriving a general formula for the area of a regular n-gon requires trigonometric analysis. Although this analysis is not fundamentally difficult, we have not yet studied the prerequisite concepts.

Practice Problem: Prove that the triangles ADE and ABC inside the regular pentagon ABCDE are congruent.

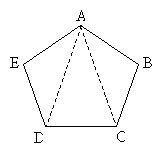
Solution: Recall that a regular n-gon is both equilateral and equiangular. Thus, we know that segments EA, AB, BC, and DE are all congruent. Furthermore, we also know that angles E and B are congruent. Let's show these facts in the diagram.

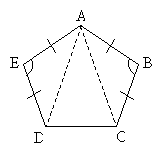
By the SAS (side-angle-side) condition, we can then conclude that the triangles ADE and ABC are congruent.

Practice Problem: What is the perimeter of a regular quadrilateral with a diagonal of length feet?

Solution: A regular quadrilateral is a square (since it is equilateral and equiangular). Let's draw a diagram of the square and its diagonal in this case. We'll also mark the sides as having length x.

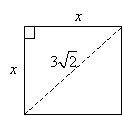
Because the diagonal forms a right triangle with legs of length x and a hypotenuse of length feet, we can use the Pythagorean theorem to calculate x.

Thus, each side of the square has a length of 3 feet. The perimeter is the sum of the lengths of all the sides-in this case, the perimeter is 12 feet.