?
In this article, we look at how to apply both vectors and the geometry of circles and triangles to uniform circular motion. Examples of such motion include the orbits of celestial objects, such as planets and stars. We derive the acceleration of such objects as well as, by Newton's second law of motion, the force acting upon them.
Key Terms
o Uniform circular motion
o Centripetal acceleration
o Centripetal force
o Tension
Objectives
o Derive a formula for centripetal acceleration of objects in uniform circular motion
o Use centripetal acceleration to solve problems involving objects in uniform circular motion
Let's Begin!
According to Newton's second law of motion, the net force acting on an object causes the object to accelerate in the direction of that net force. Cases of linear motion, such as an object that is released from some height above the ground and is allowed to fall down under the influence of gravity, are common to our daily experience. In addition, however, cases of circular motion are also common. We will consider how to approach such problems (such as the moon orbiting the Earth) and how to understand them in terms of forces, acceleration, and vectors.
If we look up into the sky (at least at certain times of the day and month), we can see the moon as it orbits the Earth. Obviously, the moon is in motion around the Earth. Because of gravity, the moon is "pulled" toward the Earth but (thankfully) doesn't ever collide with it. This situation is one example of circular motion (or nearly circular--we will assume it is sufficiently close that we can neglect any deviations from perfect circularity), where an object experiences a net force yet does not move linearly as a result. Let's take a look at why the moon moves in a circle around the Earth (and why objects in other similar situations behave as they do).
We know from Newton's second law of motion that an object experiencing a net force undergoes acceleration. In the case of the moon orbiting the Earth (or any object orbiting another object to which it is attracted by some force), the net force on the moon is always directed toward the Earth. Let's illustrate this situation by way of a diagram. The gravitational force on the moon is shown as Fg.

If both the Earth and moon were at rest initially, then the gravitational force would cause the moon to accelerate toward the Earth (with catastrophic results). But what if the moon had an initial velocity? Consider what would happen if the moon had some velocity v tangent to the surface of the Earth but no forces act on either body.
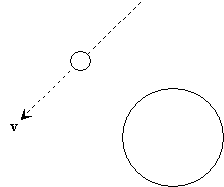
Obviously, the moon would just continue on its course, regardless of the presence of the Earth. But because the Earth exerts a gravitational force on the moon, the moon is accelerated toward the Earth. If the moon already has velocity v as shown above, the acceleration due to gravity causes the path of the moon to bend inward, as shown below.
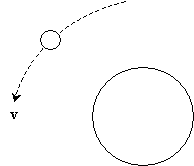
If the velocity v of the moon is too large in magnitude for a given distance from the Earth, the moon's course curves slightly, but it continues to move away from the Earth. If the velocity at that distance is too small in magnitude, the moon will eventually collide with the Earth. If the velocity is just right, however, the moon's path will curve such that it maintains a steady orbit, keeping a particular distance from the Earth at all times (such as in the current relationship of moon and Earth). Let's now consider the case where the moon maintains a consistent orbit around the Earth. An analogous situation is a ball spinning at the end of a string; both situations are shown below.
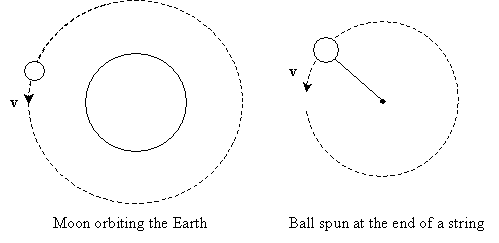
Although calculus is required to show the exact derivation of the acceleration (and thus force) acting on an object in uniform circular motion (where an object moves in a circle at a constant speed), we can nonetheless derive the correct result as follows. Let's take a look at a tiny chunk of time, ?t, during which the object in motion moves a tiny distance around its circular path. The angle subtended in this tiny portion of the path traveled is ?, and the distance of the object from the center (of its circular path) is r. Assume that the angle ? is tiny and that the drawing below is not to scale--we have made it slightly larger for clarity.
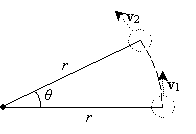
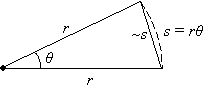
We can connect the endpoints of the radii of length r to form an isosceles triangle, as shown below. Note that if the angle ? is tiny, as we have assumed, then the arc length s is very close to the length of the unknown side of the third side of the triangle. Thus, we will simply approximate this third side as having length s as well. On the basis of circle geometry, we know that the arc length s subtended by an angle ? in a circle of radius r is simply r?.
Now, let's turn back to the velocity of the object, both initially and after a small time ?t. The acceleration of an object is just its time rate of change of velocity, which we can express as the change in velocity (?v) divided by the elapsed time (?t). In terms of v1 and v2, we can then write the following expression:
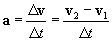
We can now apply our understanding of vectors to show v2 � v1 graphically. But because the velocities v1 and v2 are tangential to the circle and equal in magnitude, they form an isosceles triangle with an angle ? between them, as shown below.
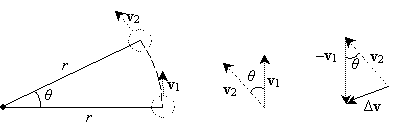
Note that because ?v is directed toward the center of motion, the acceleration is also directed toward the center (as ? gets smaller and smaller, this becomes more and more apparent--because we have used a large ? in the diagram for clarity, it appears as though ?v points is skewed slightly from the direction toward the center). Because the triangle formed by the vectors and the triangle formed by the radii of motion share the same angle ? and because both triangles are isosceles, they are similar. As a result, the ratio of r to s must be equal to the ratio of the speed v of the object (the magnitude of either v1 or v2) to the magnitude of ?v. We can then write this expression as follows:
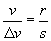
Now, since the distance traveled by the object in time ?t is s and because the object has a velocity v, we can write the following expression:
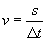
In other words, the velocity of the object is the distance s divided by the time ?t required to traverse that distance. Let's combine the preceding two expressions to eliminate s.
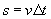
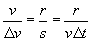
Recall our definition of a. The following is also the case (by virtue of taking the magnitude of both sides of the vector expression for a).
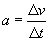
Then, further manipulating the expression above,
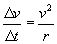
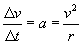
We have thus derived the acceleration of an object moving in uniform circular motion. This acceleration, ac, is called centripetal acceleration. By Newton's second law of motion, the centripetal force (Fc) is then the following for an object of mass m.
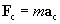
Remember that the centripetal acceleration (and thus force) is always directed toward the center of the circular path and is therefore always perpendicular to the velocity of the object. The following practice problems provide you with the opportunity to apply the results that we have derived above.
Practice Problem: The Earth has an estimated mass of 5.98 1024 kg. If it follows a circular orbit of radius 1.50
1024 kg. If it follows a circular orbit of radius 1.50 1011 meters around the sun and completes its orbit once every year (assume a year is 365 days), what is its the centripetal acceleration?
1011 meters around the sun and completes its orbit once every year (assume a year is 365 days), what is its the centripetal acceleration?
Solution: We can already state, on the basis of what we know about uniform circular motion, that the centripetal acceleration of the Earth is directed toward the sun at all times. To find this acceleration, we must use the formula we derived above:
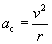
We know the radius, r, on the basis of the information provided in the problem statement. We need only calculate the velocity of the Earth. Recall that (average) velocity is simply the distance traveled divided by the elapsed time. The orbit of the Earth is equal to 2?r, and the time require for the Earth to complete this orbit is 365 days (one year). Let's convert a year into seconds so that our result will be in SI units.
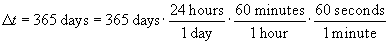
Note that each fraction on the right side is equal to unity, since (for instance) 24 hours is the same as one day.
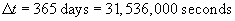
The length of the orbit, s, is the following.
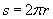
We can then write a symbolic expression for ac.
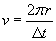
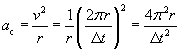
Let's plug in the numbers to get the final result.
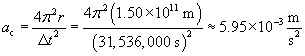
Note that the centripetal acceleration is very small--less than 0.01 meters per squared second. Yet, if we consider the mass of the Earth, we find that the force that the centripetal force (the gravitational attraction of the sun on the Earth) is huge: about 3.56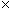 1022 newtons! (For reference, a person with a mass of 100 kg--about 220 pounds on the Earth's surface--weighs about 980 newtons.)
1022 newtons! (For reference, a person with a mass of 100 kg--about 220 pounds on the Earth's surface--weighs about 980 newtons.)
Practice Problem: A taut string (which is assumed to be massless) experiences a tension T parallel to the string and equal in magnitude to the pulling force applied to it. An object of mass 0.5 kg at the end of a string of length 0.5 meters is spun around a fixed point such that the plane of rotation is parallel to the ground. If the object's velocity is 8 meters per second, what is T?
Solution: We want to first calculate the centripetal acceleration, ac, and then the centripetal force, Fc. Let's draw a diagram of the situation. The tension T results from the object exerting a pulling force on the string (you can feel this force when you are in a turning vehicle--you feel as though you're being thrown outward!). Furthermore, the tension is equal to the centripetal force.

The centripetal acceleration of the object is the following:
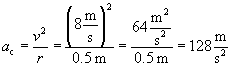
The centripetal force, and thus the tension T, are both directed at all times toward the center of the object's path. This force is the following:
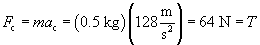
Thus, the tension on the string is 64 newtons (about 14.4 pounds of force).