Understanding Congruent Triangles
We will discuss a number of conditions that can be used to prove that two triangles are congruent (that is, prove that they are the "same" triangle), and we present intuitive geometric proofs for why these conditions work.
Key Terms
o Congruent
o Similar
o Side-side-side (SSS) condition
o Side-angle-side (SAS) condition
o Angle-side-angle (ASA) condition
o Hypotenuse-leg (HL) condition
Objectives
o Know the difference between congruent and similar triangles
o Recognize the various conditions under which two triangles are congruent and know how to justify these conditions
o Learn how to prove that two triangles are congruent
Congruence and Similarity
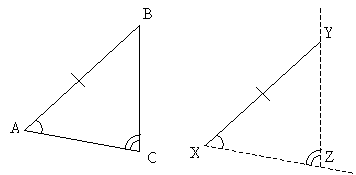
When analyzing groups of figures or figures composed of several smaller parts, it is sometimes helpful to show that two particular figures or parts of a figure are the same or similar. Doing so, in some cases, allows us to acquire additional information for our analysis. In the case of triangles, we can apply various techniques to show that two triangles are the same or that they are similar. If two triangles have sides of the same length and angles of the same measure, then we say that they are congruent triangles. The term congruent also applies to other figures: for instance, if two line segments are the same length, they are congruent, and if two angles are of the same measure, they are congruent. A pair of congruent triangles is shown below.
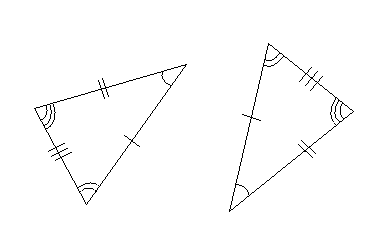
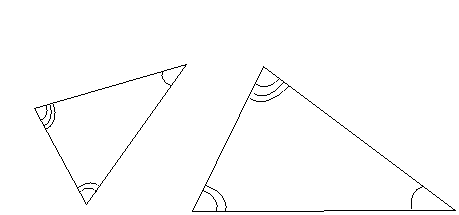
Note that although the sides are of different lengths, the same three interior angle measures are shared by both triangles. Thus, these two triangles are similar.
Proving Congruence
As mentioned above, congruent triangles must have all sides of equal length and all angles of equal measure. Nevertheless, we don't need to demonstrate all six of these relationships to prove that triangles are congruent; a number of shortcuts are available. For each shortcut, we will demonstrate intuitive reasons why it works.
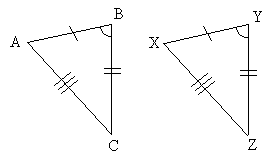
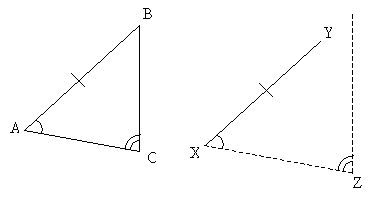
Our first shortcut to proving that two triangles (we'll use triangles ABC and XYZ for the purposes of discussion) are congruent is called the side-side-side (SSS) condition. Two triangles are congruent if their sides are all congruent. Let's take a little look at why this works. Consider triangle ABC below, and let's construct line segments that are equal to each side of ABC.

Now, consider the line segment congruent to side BC; let's attach the other two sides at either end of this line segment, but we'll otherwise leave them dangling.
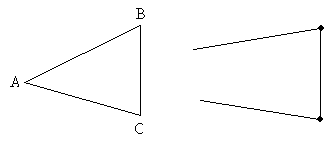

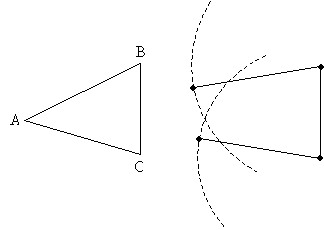
So what does this mean? Given three line segments of specific lengths, only one triangle can be formed. No matter how you move around the two dangling sides, they will only ever form one particular triangle. As a result, if two triangles have sides of the same length, they must be the same triangle (that is, they must be congruent)! As a result, triangles ABC and XYZ below are congruent.
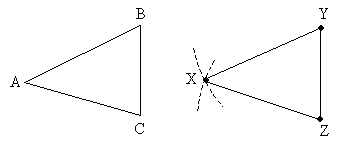

Our second shortcut is the side-angle-side (SAS) condition. Two triangles are congruent if two sides and the angle between them are the same for both triangles. We can demonstrate this congruence condition with a little more ease. Consider again some triangle ABC, and let's copy two sides (sides AB and BC) and the angle between them (angle B) and construct the corresponding figure.

Note that figure XYZ corresponds exactly to the portion of the triangle ABC that omits side AC: if we were to set XYZ on top of the triangle, they would overlap perfectly. But if we connect points X and Z, we end up with a line segment that is exactly the same length as segment AC. As such (by SSS, if you like!), the triangle that is formed, XYZ, and the triangle ABC are congruent.

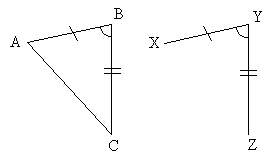
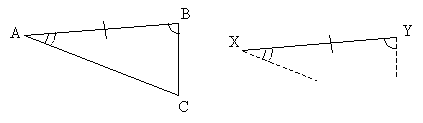
Our third shortcut to proving triangle congruence is the angle-side-angle (ASA) condition. Two triangles are congruent if two angles and the included side are the same for both triangles. Let's take a look once again at a triangle ABC, and let's construct a congruent side with two congruent angles.

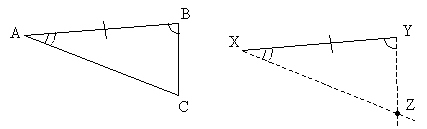
The side XY is the same length as side AB, and the angles A and B have the same measures as angles X and Y. The dashed line segments are defined by the angles. Two non-parallel and non-coincident lines only intersect at one point, so two angles and an included side determine one and only one triangle.

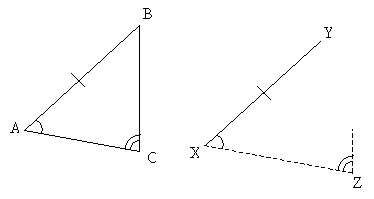
As a result, triangle XYZ and triangle ABC are congruent.
Our last general shortcut for proving congruent triangles is the angle-angle-side (AAS) condition. If two triangles share two angles of the same measure as well as one side (not included by the angles) of the same measure, the triangles are congruent. Let's consider our triangle ABC and let's copy two of the angles and a non-included side.

The dashed lines in figure XYZ indicate lines whose lengths we do not yet know. Nevertheless, because of the angles that must be as shown, we know that the remaining sides of the triangle must be parallel to (in the case of YZ) or coincident with (in the case of XZ) the dashed lines. Let's extend the line segment from Z. Although it doesn't intersect Y, we can then adjust the length of XZ until it does.

Then,

What we have shown here is that only one length of segment XZ will form a triangle, given side XY and angles X and Z. As a result, two angles and a non-included side determine exactly one triangle, and therefore, triangles ABC and XYZ above must be congruent.
These illustrations should help demonstrate why each of these four general conditions proves the congruence of triangles in general. A special case for proving congruence involves right triangles: the hypotenuse-leg (HL) condition. Recall that if we know two sides of a right triangle, we can use the Pythagorean theorem to calculate the length of the third side. As a result, if two right triangles both have a hypotenuse and a leg of the same lengths, the remaining leg must be the same length for both triangles as well. Then, by our SSS condition, the two triangles must be congruent.
Practice Problem: Using the four general conditions for triangle congruence (SSS, SAS, ASA, SSA), prove the HL condition.
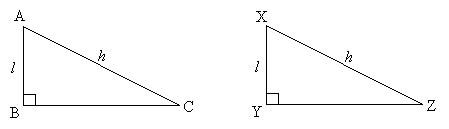
Solution: We can apply our techniques of geometric reasoning to solve this problem. Let's use a two-column proof format to clearly outline our reasoning, and let's start by drawing two triangles, ABC and XYZ. Notice that we label the hypotenuses XZ and AC as having length h, and the shared legs AB and XY as having length l.

The two-column proof format would then be as follows (note that we use the symbol ![]() to indicate congruence).
to indicate congruence).
1. AB![]() XY Given
XY Given
2. AC![]() XZ Given
XZ Given
3. BC = ![]() Pythagorean theorem
Pythagorean theorem
4. YZ = ![]() Pythagorean theorem
Pythagorean theorem
5. BC![]() YZ Statements 3 and 4
YZ Statements 3 and 4
6. ABC![]() XYZ SSS condition (statements 1, 2, and 5)
XYZ SSS condition (statements 1, 2, and 5)
Note that for statements 3 and 4 we used the Pythagorean theorem to algebraically calculate the lengths of BC and YZ; even though we do not have fixed numbers, the expressions are still identical given h and l. Thus, we have proven, using one of our four general conditions (SSS), that the HL condition is a valid way to prove the congruence of two right triangles.
Practice Problem: Prove that triangles MNO and MPO are congruent.
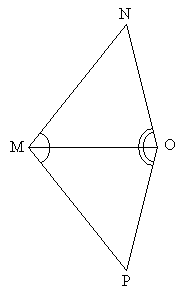

Solution: Once again, let's use a two-column proof to illustrate our reasoning. First, we know that the line segment MO is congruent with itself (thus, triangles MNO and MPO have a congruent side-we can call this property identity). We also know that the triangles have two congruent angles that share the segment MO: angles PMO (which we can write as ![]() ) and NMO (which we can write as
) and NMO (which we can write as ![]() ), as well as angles NOM and POM (
), as well as angles NOM and POM (![]() and
and ![]() ).
).
1. MO![]() MO Identity
MO Identity
2. ![]() Given (in figure)
Given (in figure)
3. ![]() Given (in figure)
Given (in figure)
4. ![]() ASA condition
ASA condition
Thus, we have proven using ASA that the two triangles are congruent. (Note that in statement 4, we use the triangle symbol to indicate a triangle, as opposed to an angle.)
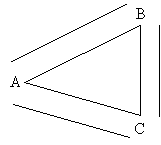
Practice Problem: Assuming line segments AB and DC are parallel and sides AD and BC are parallel, prove that triangles ABC and ACD are congruent.
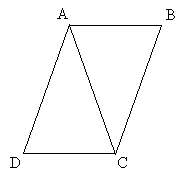

Solution: Because this figure involves parallel line segments, we can apply what we know about parallel lines cut by transversals. The corresponding angles inside the figure are shown below.
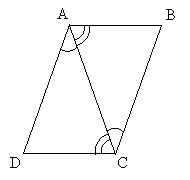

1. ![]() Identity
Identity
2. ![]() Corresponding angles
Corresponding angles
3. ![]() Corresponding angles
Corresponding angles
4. ![]() ASA condition
ASA condition
Thus, we see how we can apply a number of different geometric concepts that we have studied thus far to prove relationships between figures.