Key Terms
Objectives
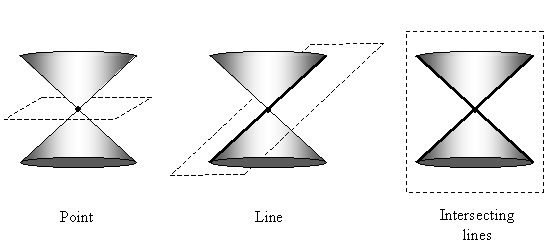
As it turns out, quadratic functions can be related to a broader class of algebraic relations known as conic sections. Here, we will delve briefly into some of the different conic sections and their properties.
Introduction to Conic Sections
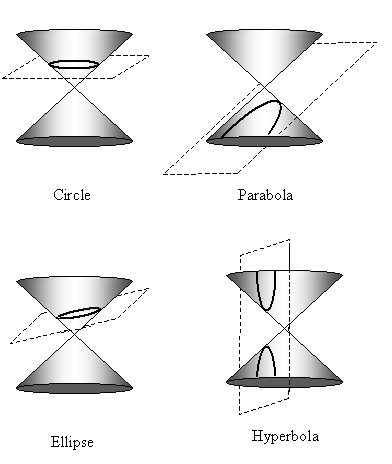
Two familiar (non-degenerate) conics are the circle and the parabola. A parabola is the shape of a quadratic polynomial.
Conic sections all obey the algebraic expression below, where A, B, C, D, E, and F are constants.
This expression is even more familiar if E = -1.
Conics: Circles and Parabolas
Having introduced how the conic sections are related to cones and the overall algebraic expression uniting them, we now turn to look at specific algebraic relations for each conic. First, consider the circle, whose general equation is given below.
Note that this expression is very similar to the Pythagorean theorem, from which we can obtain the equation of a circle centered on the origin:
The more general expression clearly describes a circle with a radius r, but what about the meaning of h and k? As it turns out, (h, k) is the center of this circle. Thus, for example,
describes a circle of radius 2 centered at (1, –1). The graph of this relation is shown below.
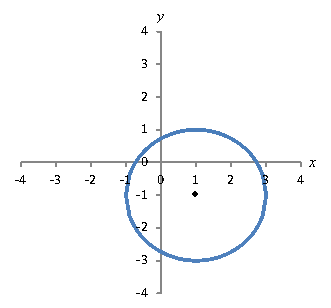
Practice Problem: Draw a graph the following conic section and solve for y(x): 
.
Solution: Since, by the form of this expression, it is clear that the graph is a circle centered at (3, -2) and with a radius of 1, you need not plot a number of points. Instead, you can simply sketch the circle.
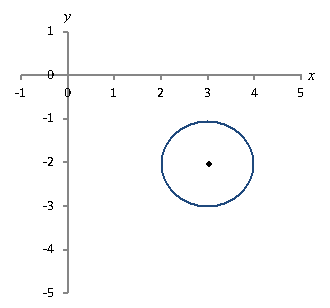
Now, we can also solve for y to write the expression in the more familiar form of an algebraic relation--that is, y(x) = some expression in x. Note carefully the need for the ± symbol when taking the square root.
Another familiar conic, the parabola, obeys the relation below.
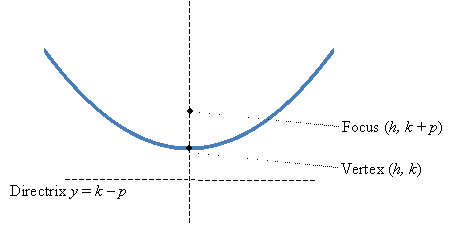
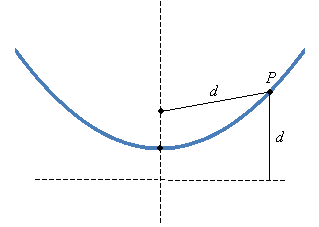
The vertex of the parabola is clear enough: it is the bottom point of the "trough," and it is located at (h, k). The focus and directrix of the parabola are related as follows: the distance from the focus to any point P on the parabola is equal to the vertical distance from P to the directrix. This is illustrated below.
A parabola can also be oriented horizontally. In this case, the algebraic expression is
where the vertex is still (h, k), but the focus is (h + p) and the directrix is x = h – p.
Parabolas find application in antenna dishes. A typical antenna dish has a three-dimensional parabolic shape, and the receiver/transmitter is placed at the focus. This arrangement has the advantage that incoming (parallel to the vertical axis) electromagnetic waves that strike the dish are all reflected to the focus. Likewise, waves emitted from a transmitter placed at the focus are reflected outward by the dish, parallel to the vertical axis. This latter case is illustrated below; for reception of electromagnetic waves, simply reverse the directions of the arrows.
when oriented vertically. (All numbers and variables are measured in feet). To maximize reception of incoming waves parallel with the vertical (y) axis, how far from the vertex of the dish should the engineer place the receiver?
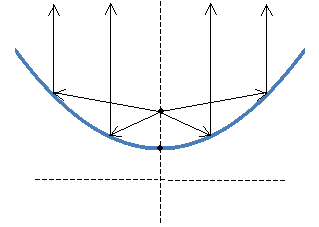
Solution: One approach is to relate this expression to the standard algebraic form of a vertically oriented (i.e., opening upward in the +y direction) parabola:
Thus, we can see in this case that the vertex of the parabola is (0, 0), and p = 3. The focus of the parabola--the best location for the receiver in a parabolic-dish antenna--is 3 feet from the vertex (measured along the vertical axis).
