Objectives

Circles and Trigonometry

 

 

 

 

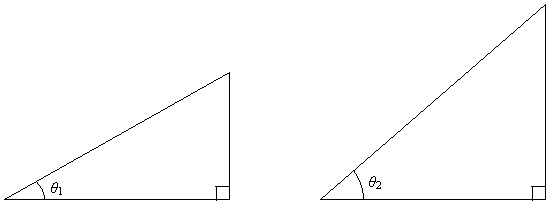
For simplicity, let's fix the hypotenuse of the triangle at a given length: we'll call it r for now. We'll call one of the acute angles θ (the other acute angle is 90° – θ.)

As we vary the angle θ, the opposite and adjacent sides of the triangle also vary.

 

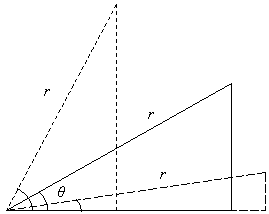
At this point, you might note that as we "rotate" the hypotenuse of length r, we end up with a circle. The circle has a radius r, and its center point is the vertex corresponding to the angle θ.

 

 

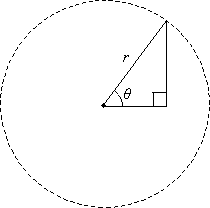
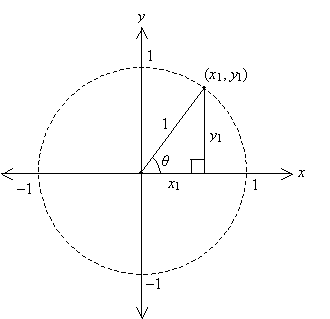
If we overlay a set of coordinate axes on this circle, with the origin on the center, we see that the adjacent side of the right triangle is a distance along the x-axis and the opposite side is a distance parallel to the y-axis. Furthermore, the vertex of the triangle on the circle must have coordinates (x₁, y₁), where x₁ is the length of the adjacent side and y₁ is the length of the opposite side.

 

 

 

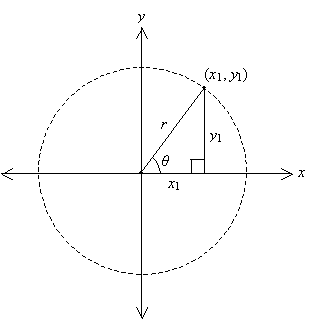
By the Pythagorean theorem, we know the following relationship among r, x₁, and y₁.

 

If we "normalize" the hypotenuse to a length of 1 (that is, set r equal to 1), then we call the resulting circle a unit circle. In this case, the circle intercepts the axes at y = ±1 and x = ±1.

 

So what does this all do for us? Why should we care? Well, first, notice that we've joined our concepts of coordinate graphs, circles, and right triangles together--they are interrelated. Thus, logically, we expect trigonometry to have a role in our understanding of circles as well as right triangles. But before we delve further into this relationship, we must first define some properties of the angle θ in this context.

 

 

 

Angle Measurements

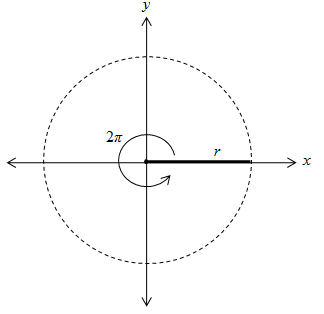
Thus far, we have relied exclusively on degrees as the unit of angle measure. Another unit with which you should be familiar is the radian. First, note that the circumference of a circle is 2πr, where r is the radius. If we divide out the radius from the circumference, we are left simply 2π: this is in some sense how "far" the circle goes around its center, regardless of the radius. In other words, 2π is the angle swept by the radius of the circle.

 

 

As you probably recognize, then, 2π is also equivalent to 360°. The unit of angle in this case is the radian. One radian is defined as the angle formed such that the portion of the circle (or arc length ) swept by that angle is equal to the radius of the circle.

 

 

 

 

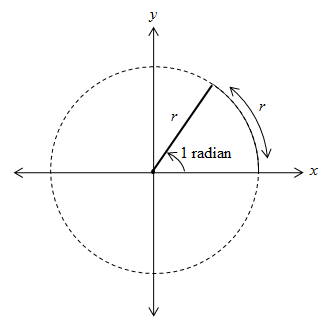
Another way to look at it is this: if we took a segment of length r (the radius) and molded it onto the circle, the angle formed by the radii connecting the center of the circle to the endpoints of the arc would have a measure of 1 radian. As it turns out, one radian is equal to approximately 57.3°.

 

 

By convention, the angle θ is measured from the x-axis in the counterclockwise direction. If the clockwise direction is used, the angle is simply assigned a negative value. Thus, for instance, π radians (180°) and –π radians (–180°) correspond to the same point on the circle.

 

 

 

 

 

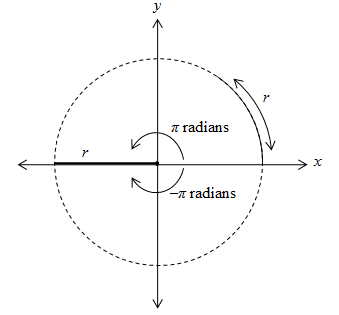
For our purposes, we will primarily deal with angles between –2π and 2π, inclusive (that is, –2π ≤ θ ≤ 2π). Angles larger in magnitude than 2π are defined, but they overlap with lower-value angles, so we won't consider them in much detail.

 

 

Practice Problem: Convert each of the following angle measures to radians. Be sure to use exact expressions for your answers.

 

a. 60° b. 270° c. -90° d. 120°

 

 

Solution: First, note that 360° is equal to 2π radians. We can use this ratio to convert from degrees to radians. Below is the calculation for part a; the other parts follow the same pattern. Note that the negative sign (part c) translates directly from degrees to radians.

 

 

a. b. 3 Pi / 2 radians c. -Pi / 2 radians d.

 

 

Practice Problem: Convert each of the following angle measures from radians to degrees.

 

 

a. b. c.

 

 

 

Solution: Here, simply use the same process as the previous practice problem, but use the reciprocal ratio of radians and degrees. Again, only the calculation for part a is shown below; the rest are similar.

 

 

 

a. -22.5° b. 360° c. 36°

 

 

Application to Trigonometric Functions

 

Now, we can finally look at what circles have to do with trigonometry. Let's look again at our unit circle.

 

 

 

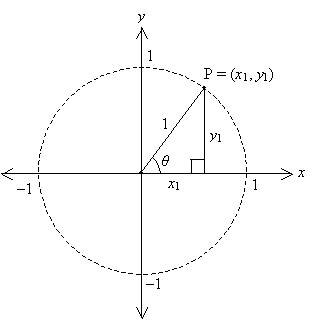
Each point P on the unit circle, designated by the coordinates (x₁, y₁), can be expressed in terms of the angle θ as well. Note the following, where we apply what we learned about right-triangle trig:

 

 

 

 

 

 

 

In other words, point Phas coordinates (cos θ, sin θ), where θ is the angle formed between the x--axis and the radius to P. What we've also done is define two functions:

 

 

 

sin θ = distance of point P from the x-axis

 

cos θ = distance of point P from the y-axis

 

 

 

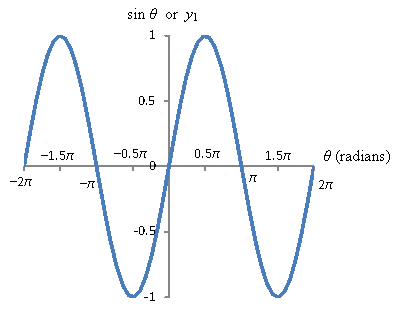
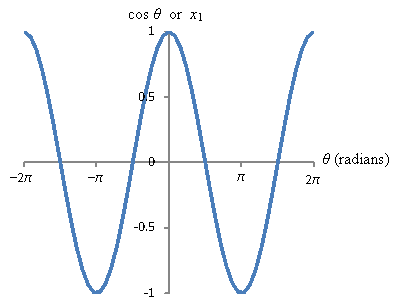
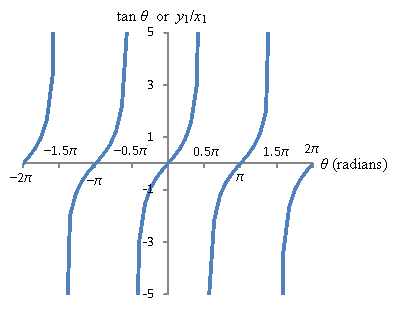
The tangent of the angle, tan θ, is simply the ratio of these distances (specifically, ). As the angle θ changes, these distances change; we can plot them graphically, however, to see how they behave. Below are the sine, cosine, and tangent functions plotted for the θ domain [-2π, 2π]. Note that to compute trig functions using radians instead of degrees, you must make sure your calculator is in radian mode, not degree mode.

 

 

 

 

 

 

 

 

 

 

 

 

Practice Problem: A tire has a radius (outer radius) of 10 inches. A small mark is painted at the very top of the tire, and then the tire is rolled forward slightly so that the mark rotates through an angle of pi/4 radians. How far above the ground is the mark at this point?

 

 

 

Solution: This problem requires that we apply much of what we've learned. First, draw a "tire" (circle) with a radius of 10 inches, and draw a point at the top of the tire to indicate the mark.

 

 

 

 

 

 

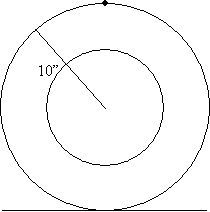
Now, let's "rotate" the tire by radians (also equal to 45°). We'll show the mark at its original position and its new position. (We omit the "inner circle" of the tire for clarity.)

 

 

 

 

 

 

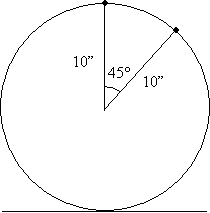
We can use the basic facts of angles to redraw this situation in a more familiar form.

 

 

 

 

 

 

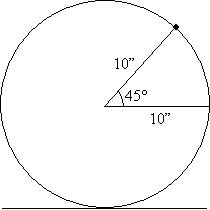
Now, we want to find the height of the mark above the ground. Using the definitions in the figure below, this height is 10 + y.

 

 

 

 

 

 

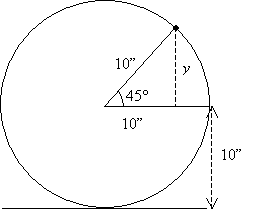
Our job is to then calculate y. We can use trigonometry as follows.

 

 

 

 

 

 

 

Thus, the mark is about 17.07 inches above the ground.