Math Skills: How to Do Division

Grouping of Objects

Division can be considered to be the opposite or inverse of multiplication. If we go back to the 12 dogs in multiplication, we can divide them into 3 equal groups. How many will be in each group?

12 Dogs total, placed into 3 groups of 4:

Group 1

Group 2

Group 3

4 Dogs

So now we can say that 12 dogs divided into 3 groups is 4 dogs per group. We can write that as --

12 3 = 4 (here we use the division symbol)

12 / 3 = 4 (the slash indicates ‘divided by')

Terms – Divisor, Dividend, Quotient, Remainder

There are four main terms to describe the parts of division. The dividend is the number that is being divided. The divisor is the number that will be doing the dividing. The quotient is the answer, or the number of times the divisor goes into the dividend. In the problem, 12 3 = 4, 12 is the dividend, 3 is the divisor and 4 is the quotient.

If we have the problem 23 5 = 4 R 3, we have a dividend of 23, a divisor of 5, a quotient of 4, and a remainder of 3 because 23 cannot be divided equally into 5 groups. When you divide it into 5 groups, you get 4 in each group and 3 objects left over.

Division Facts

Division is quicker and easier once you know and memorize the basic facts. The division facts are the inverses of the multiplication facts. For example, if 9 x 6 = 54, then 54

9 = 6.

Flash cards are a great aid in learning division facts.

Division by Zero - Undefined

Division is defined as the inverse of multiplication. If 2 x 9 = 18, then 18

9 = 2 and 18

2 = 9.

Division by zero would be the inverse of multiplying by zero. 7 x 0 = 0. This corresponds to 0/7 = 0 or 0 7 = 0. However, 0 0 is not 7. This does not compute. So division by zero is undefined since it does not work with our definition.

Division of zero is considered undefined. It is impossible to divide nothing into groups of nothing.

Multiplication Identity Element - One

An identity element is a specific number that when put with any other number in a specific way gives the original number. One is the multiplicative or multiplication identity element. It is also a division identity element. One times any number is the original number; an original number divided by one is the original number.

a x 1 = a
5 x 1 = 5 and 25 x 1 = 25
A 1 = a
5 1 = 5 and 25 1 = 25

Multiplicative inverse

A multiplicative inverse, or reciprocal, for a number (such as a) is denoted by 1/a such that the number, a, and its reciprocal, 1/a, yield 1 when multiplied.

Want to learn more? Take an online course in Basic Math.

For example, the multiplicative inverse of 8 is 1/8. When you multiply 8 x 1/8, the answer is 8/8 which is 1, or 1 whole.

For the multiplicative inverse or reciprocal of any number, divide 1 by that number.

Division with a Single Digit Divisor

When we actually do division, we have to use what is called long division. Let's divide 46 by 2.

We can ask: how many times does 2 go into 4 or 4 divided by what equals 2. We know that 2 x 2 = 4. Therefore, we put a 2 above the 4, then we multiply that 2 times the 2 in the divisor and get 4 which we put under the 4 and subtract.

When we subtract, the answer must always be less than the divisor. If it is not, you know that the digit you used in the quotient can be increased by at least one. Also check your multiplication and your subtraction.

Now we bring down the 6 and ask what we get when we divide 6 by 2. It is 3. So we put the 3 above the 6 and multiply it times the 2 in the divisor to get 6 and then subtract.

To check your answer, multiply the quotient by the divisor. If the dividend is your answer, your quotient is correct. 2 x 23 = 46.

This is a fairly simple problem which works out evenly. Let's try a problem which is not so straightforward. Let's divide 3,749 by 3.

The 3 goes into the 3 (for 3,000) once, so put a 1 above the 3 and multiply 1 x 3 to get 3 and subtract. Then bring down the next digit.

How many times does 3 go into 7? We know that 3 x 2 = 6 and 3 x 3 = 9. We cannot go over 7, so we put the 2 above the 7 and multiply, putting the 6 below the 7 and subtracting to get 1. Then bring down the 4.

Now we need a number that when multiplied by 3 gives us the closest number to 14 without going over. 3 x 5 = 15, so that is too much. 3 x 4 = 12, so we use 4 above the 4, and put the 12 under the 14 and subtract to get 2. Then we bring down the 9.

How many times will 3 go into 29? 3 x 9 = 27. So we will put the 9 above the 9, multiply and subtract again. Since we have no more digits to bring down, we will have a remainder of 2.

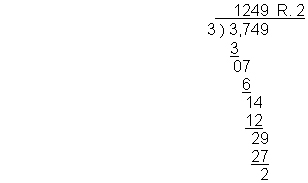
In real life situations, a remainder does not work out very well. When you start to do decimals, you will use another method to work with remainders.

To check your answer, multiply the quotient by the divisor, then add the remainder:

1249 x 3 = 3,747 + 2 = 3,749

Division with a Multiple Digit Divisor

Sometimes your divisor has two or three digits. This really isn't difficult to work with; it simply takes a little more thought. Let's look at 2,892

12.

Now you have to start with the first two digits of the dividend (sometimes you have to look at three at a time). How many times can 12 go into 28 without going over 28? 2 x 12 = 24 and 3 x 12 = 36. Therefore, we will put a 2 above the 8 and multiply 2 x 12 = 24 and put the 24 under the 28 and subtract to get 4. Then we will bring down the next digit which is a 9.

We know that 4 x 12 is 48, so we put a 4 above the 9. Then we multiply and put the 48 below the 49, subtract to get 1 and bring down the 2 to go with it.

This is the same number as our divisor, so we put a 1 (multiplicative identity element) above the 2, multiply and subtract to get 0.

**Remember that when you subtract, the number you get must always be smaller than the divisor. If it is not, then you need to increase the digit in the quotient by 1 and multiply again. Also, the remainder must always be less than the divisor.

Divisibility Rules

1. A number is evenly divisible by 2 if it ends in 0, 2, 4, 6, or 8.

2. A number is evenly divisible by 3 if the sum of the digits is a multiple of 3.

3. A number is evenly divisible by 4 if the lasts two digits are a number that is a multiple of 4.

4. A number is evenly divisible by 5 if it ends with 5 or 0.

5. A number is evenly divisible by 6 if the sum of the digits of the number is a number that is a multiple of 3 and the last digit is an even number (divisible by 2).

6. A number is evenly divisible by 9 if the sum of the digits are a multiple of 9.