What is Geometry?

Key Terms

o Geometry

o Planar geometry

o Solid geometry

o Euclidean geometry

o Figure

o Point

o Line

o Dimension

o Ray

o Plane

Objectives

o Know why geometry is important both in academic and professional settings as well as in daily life

o Recognize several fundamental geometric figures and how to draw representations of them

Introduction to Geometry

Although the mathematical jargon, concepts, and tools of geometry may not yet be familiar to you, chances are you have used geometry regularly in your everyday life. Anyone who has measured the length of some object, attempted to "level" a painting on the wall, or tried to build something so that it is "square" has used geometry. The study of geometry allows us to apply mathematical rigor to many of these daily activities that involve length, parallelism (for instance, making a picture or painting level with the floor), angles, areas, volumes, or a variety of other parameters. This goal is to teach you the mathematical foundation of geometry, which will give you the ability not only to perform many daily tasks with a new rigor and understanding, but also to gain knowledge that you can extend into other fields of math and science.

Numerous occupations and fields of study rely heavily on geometry. Construction, for example, requires a solid understanding of lengths, angles, areas, and other geometric parameters. The natural sciences also require a solid understanding of geometry; in physics, for instance, geometric reasoning and calculation are an integral part of solving a wide range of problems. Anyone interested in these or any number of other areas of work or study can benefit from a solid and rigorous understanding of geometry.

Interested in learning more? Why not take an online Geometry course?

Geometry is the study of the relationship, properties, and measurement of figures (such as points, lines, and planes) in a space with an assumed set of characteristics. Thus, the study of geometry starts with various assumptions about the space in which various figures exist, then it goes on to deduce conclusions about those figures. To be sure, this approach, upon reflection, sounds daunting, but it need not be so. If you've ever heard the statements "the shortest distance between two points is a straight line," then you already have some inkling about the characteristics of a type of geometric space. (Strangely, in certain geometric systems or spaces, the shortest distance between two points is not a "straight line" in the colloquial sense of the phrase!) We're going to deal primarily with so-called planar geometry, which is a geometric system (or space) that closely follows many of what we might consider "common sense" rules about the relationship of figures, such as lines (for instance, two lines that do not intersect are parallel). Planar geometry, as the name indicates, deals only with two dimensions (left and right, forward and backward, for example). Solid geometry is an extension of planar geometry that adds a third dimension (up and down, if we follow the orientation example for planar geometry). These two geometries are aspects of the more general Euclidean geometry, which is a term sometimes applied to either planar or solid geometry.

Fundamental Geometric Figures

When studying geometry, we will deal with several fundamental figures, including points, lines, and planes. A point can be thought of as an infinitesimally small sphere; that is, if you consider a "round" object such as a tennis ball, imagine that ball getting smaller and smaller until it is so small that it cannot be measured or even seen--this is akin to a point. A point has no width, length, or depth. A point can also be thought of as simply a location; a location does not have any physical dimension such as length or width, and yet we know intuitively how to speak of locations: "no trespassing beyond this point," for instance. Even though a point has no measurable size, we still need a way to represent it when studying geometry. Thus, we typically represent points as small dots, such as those shown below.

A line has slightly more character than a point: it is a figure that extends infinitely in one dimension. (A dimension can simply be thought of as a pair of opposite directions: forward and backward, left and right, or up and down, for example.) A line has infinite length, but it has no thickness. Imagine a piece of string that is pulled tight from two points that are immeasurably far away, and imagine that the thickness of the string decreases until the string is invisible: this string would then be a line. Because we can't show infinite distances on a piece of paper (or anywhere else, for that matter), we use arrows when drawing lines to indicate that the figure extends indefinitely. Below is an example of a line.

Naturally, we can conceive of a line that extends to infinity (that is, extends indefinitely) in only one direction but has an end point in the other direction; this figure is called a ray. Imagine the sun shining in the sky--a beam of light that originates from the sun can extend indefinitely away from it. The word "ray" in this case is closely linked with the geometric figure called a "ray." A ray is illustrated below.

If the line instead has two endpoints, we call it a line segment, which is illustrated below.

In some cases, it is helpful to show the endpoints of the ray or line segment more clearly using dots. The figures are the same, however.

A plane is a geometric figure that extends to infinity in two dimensions. As such, we must show it in three dimensions, but you can imagine a plane as an even surface whose edges are so far away that they could never be reached. Planes are often drawn as parallelograms (four-sided figures similar to rectangles), since their infinite extent cannot be represented. We will draw the plane with a dashed border to differentiate it from a parallelogram.

Because we will mostly deal with (two-dimensional) planar geometry, we will not deal much with planes. Note, however, that we are in a sense dealing with a plane in planar geometry: we do all our drawing, moving, and analyzing of figures located entirely on that one plane. Consider, for instance, the collection of basic figures shown on the plane below.

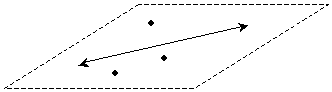
Now that we have a set of fundamental geometric figures, we can begin to analyze and combine them to discover their relationships as well as the properties of more complicated figures, such as polygons and circles.

Practice Problem: Determine whether three points always lie on a single line.

Solution: This problem begins to get you thinking about geometry. Although we have not introduced any rigorous method for proving mathematical propositions, we can still think this problem through by just working with the figures we discussed in the article. We can imagine that any two points can always lie on some single line (after all, "the shortest distance between two points is a straight line!"). Let's draw this situation:

No matter where the two points are, we can always draw a line (or line segment) that connects them. (Another way of saying this is that two points determine a line.) What if we add a third point? We can add the point on the line or off it, as shown below.

Let's consider the point not on the line. Regardless of the line that we draw to connect any pair of points, the third point is not on the line, as illustrated below.