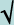In addition to reviewing the simple arithmetic mean (average), we also introduce the geometric and power means and briefly discuss how these means can be used to characterize the central tendency of data.
Key Terms
- Mean
- Arithmetic mean
- Average
- Population
- Population mean
- Sample
- Sample mean
- Geometric mean
- Power mean
- Root mean square
Objectives
- Review arithmetic means and some associated concepts in descriptive statistics
- Consider other types of means, including geometric and power means
Let's Begin!
Let's review review descriptive statistics, since the formulas and meaning of these statistics plays a critical role in understanding applied statistics.
Later, we will consider more-advanced topics such as linear regression, correlation, Student's t-tests, ANOVA analysis, repeated measures, and other topics. These higher-level topics apply basic statistical theory to problems that involve more than, for instance, simple calculation of means and variances. Although this by no means provides a complete survey of advanced statistical theory and the tools used therein, in does provide a solid overview of how statistics can be used to perform more-refined analyses of data sets.
This article considers discrete data sets (or distributions), rather than data sets containing continuous data sets (distributions). Thus, the mathematical formulas rely almost exclusively on summations ( Σ ) rather than integrals ( ∫ ). The same principles apply in both cases, however, and the conversion of the formulas from the discrete (summation) form to the continuous (integral) form is usually fairly straightforward.
At this point, we now turn to a review of descriptive statistics.
Arithmetic Mean
A mean is a statistical value that describes the "central tendency" of a data set. The term mean usually refers to the arithmetic mean, or the average. Not all means, however, are arithmetic means. Nevertheless, the arithmetic mean is often used, and its mathematical definition is quite useful. Calculating the arithmetic mean simply involves adding all of the numbers in a data set and then dividing by the number of members. In the formula below, the data set is assumed to have N members, with the ith member identified as xi. (Thus, the data set could be written as {x1, x2, x3,., xN}.)
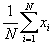
If the data set contains all possible members of a particular group, then that data set corresponds to a population and the mean to a population mean. Population parameters are typically identified using Greek characters; in the case of the mean, the symbol μ represents the population mean:
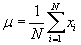
For example, if we were to calculate the mean height of people in a particular room of a building, a population mean would likely be possible, since measuring the height of each person is probably feasible. If we wanted to calculate the average height of all people on Earth, however, we would run into a problem: measuring every person's height is a near impossibility. In this case, we might instead collect a sample of the population, which is a data set that only contains a portion of the data representing the entire population. The mean of this data set is the sample mean. Sample statistics are often represented using Roman characters; in the case of the sample arithmetic mean, we will use the notation 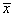 to represent the sample arithmetic mean. In the slightly modified formula below, k represents the number of elements (or members) in the sample (N is still assumed to be the number of elements in the population-thus, k < N).
to represent the sample arithmetic mean. In the slightly modified formula below, k represents the number of elements (or members) in the sample (N is still assumed to be the number of elements in the population-thus, k < N).
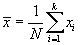
Practice Problem: A forester wants to describe a large area of forested land by the age of a certain species of tree. She collects samples from the trees and determines that the ages (in years) are the following:
{104, 97, 86, 115, 34, 87, 59, 68}
What is the average age of the species, assuming that this data is representative?
Solution: Note that the data, in all likelihood, corresponds to a sample rather than the population. Although this distinction does not affect the calculation of the arithmetic mean, it can have an effect on other descriptive statistics, such as variance. Calculate the mean as follows, noting that the data set contains eight elements:
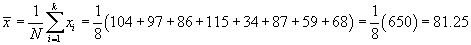
Thus, the trees have a mean age of about 81 years.
Other Means
As mentioned above, the use of the term mean generally refers to an arithmetic mean. Nevertheless, other types of means can be calculated as well. In some cases, slightly different definitions of the mean are needed to accurately represent the central tendency of a data set. Consider, for instance, the context of finance: an investment might grow by various percentages (or ratios) over several years. The percentage growth of the investment over several years might be the following:
{5%, 7%, 9%, 4%, 5%}
In other words, the investment grows by 5% the first year, 7% the second year, and so on. Because the amount in the investment changes every year, calculating the final amount requires calculating a product rather than a sum. For an initial investment P, the final amount F after five years is the following:
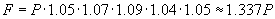
The total growth of the investment is therefore about 33.7%-significantly more than the sum of the individual percentages (5% + 7% + 9% + 4% + 5% = 30%). To calculate a mean that recognizes this fundamental difference, we define the geometric mean, which calculates a mean based on multiplication of the data elements rather than addition. The arithmetic mean μ is defined such that for a set of N data elements, the product Nμ is equal to the sum of those elements. For the geometric mean GM of a data set with N elements, GM N is equal to the product of those elements. Thus, for a data set {x1, x2, x3,., xN},
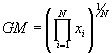
Note that the capital pi implies multiplication, just as the capital sigma in the formula for the arithmetic mean implies addition. For our financial example, then, the geometric mean is the following.
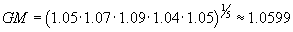
Here, we use the numbers 1.05, 1.07, and so on in calculating the geometric mean rather than just 0.05, 0.07, and so on, because these are growth rates. (The principle is multiplied by 1.05, not 0.05, for instance.) Generally, however, the geometric mean for an arbitrary data set {x1, x2, x3,., xN} uses the formula given above.
The geometric mean growth of the investment, therefore, is very nearly 6%. Note that if we multiply the initial investment P by GM raised to the fifth power, we get the same final investment value (the slight difference is due to rounding):
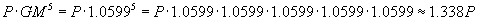
Practice Problem: Calculate the geometric mean of the following data set:
{0.75, 1.22, 1.09, 0.98, 1.35, 1.29, 0.95}
Solution: Use the formula for the geometric mean; in this case, the data set has seven elements.
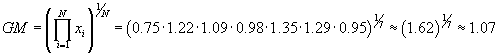
(Using a radicals calculator, enter the power 7 and the product 1.62 to get 1.07)
|
|||||||||
Thus, the geometric mean of the data is 1.07 (note that this is significantly different than the average value of 1.09).
Another mean is the so-called power mean, which has the following form for a data set {x1, x2, x3,., xN} and an arbitrary power p:
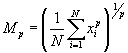
As it turns out, this is a general form of the mean that can be used to express arithmetic, geometric, and other means when the correct value of p is used. For instance, consider the case of p = 1:
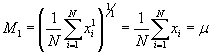
Again, this is simply the arithmetic mean. Using p = 2, we can calculate the root mean square of a data set:
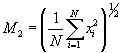
Notice that the root mean square is simply the square root of the arithmetic mean of the squares of the data set-hence the name. The root mean square is a tool often used in physical sciences and engineering, for instance, to characterize the magnitude of a varying value.
Practice Problem: A scientist measures a certain parameter's variation from the expected results. Use the root mean square to determine the average variation of following measured data.
{1.0, -2.2, 3.2, 0.5, -1.6, -1.8, 0.1}
Solution: The root mean square is the power mean for the case of p = 2. The root mean square allows us to calculate a mean variation despite the presence of negative numbers (which would tend to make an arithmetic mean show a smaller variation than is actually present).
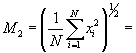
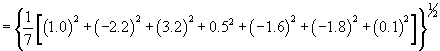
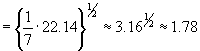
Thus, the root mean square of the variation is 1.78.