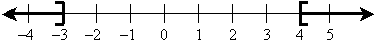• Equation
• Solution
• Solution set
• Inequality

Objectives

• Review the fundamentals of equations and inequalities and their solution
• Solve equations and inequalities to find and graph their solution sets

Introduction to Equations

We've seen numerous examples of functions, which relate the value of an dependent variable to some expression (an algebraic relation obeying the vertical line test) involving an independent variable. But in mathematics (and its various applications), we often run into cases where two functions are related by way of an equals sign (=); such expressions are called equations. For instance, let's say and . The following is an example of an equation:

Because of our definitions of the functions f and g, we can equivalently write

This is an equation in one variable, since only one variable appears in the expression. In a sense, then, and are also equations (since they involve the equal sign), but they are equations in two variables (the dependent and independent variables).

A solution to an equation is a value of the variable (or variables) that satisfies the equation. Consider our example above: x = –1 is a solution to the equation because it maintains the equality when substituted into the expression:

This final statement, 1 = 1, is obviously true, so x = 1 satisfies the equation. On the other hand, x = 1 is not a solution of the equation, since substitution of x = 1 into it yields a contradiction (falsehood):

Obviously, 1 is not equal to –3, so x = 1 fails to satisfy the equation. Graphically, the solution set for an equation is the set of values corresponding to the intersection points of the two expressions. Again, consider the above example equation; a plot of the two functions f and g is shown below.

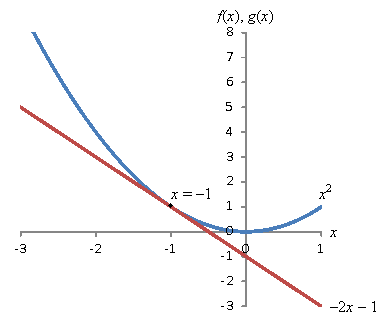
Note that an equation in one variable has a solution set (the set of all values for the variable that satisfy the equation) that comprises individual values for the lone variable; an equation in two variables, on the other hand, has a solution set that comprises ordered pairs of values. In the case of , the "solutions" are the set of ordered pairs , which we can also write as . But these ordered pairs are the same as the points on the graph of the function!

For our purposes, we will generally be dealing only with equations in one variable, but it is worthwhile to note the above-mentioned relationship between what you might already understand to be a solution (given a single-variable equation) and a solution for a function definition or multivariable equation. In addition, we'll assume that you're already familiar with methods of solving simple equations (like linear and quadratic equations).

Practice Problem: Find the solution set for the equation .

Solution: To find the solution set, we need to determine all values of y that satisfy the equation . You may be able to determine the solution set in this case by inspection; below, however, is the more formal approach.

Thus, the solution set for the equation is the set of y values {–3, 3}.

Practice Problem: Find the solution set for the equation 3z - 4 = 8z.

Solution: Again, use the standard algebraic approach to isolate the variable. In this case, the equation only has a single value in the solution set.

Remember that you can check your solution by plugging the obtained values back into the equation. If the equation is not satisfied, then you've made a mistake in your work!

Introduction to Inequalities

Inequalities are almost identical to equations, except that they involve the symbol < ("less than"), > ("greater than"), ≤ ("less than or equal to"), ≥ ("greater than or equal to"), or some combination thereof. The approach to solving an inequality is similar to that of solving an equation, but the solution set is often (but not always) a range of values rather than a set of discrete values. Some care is required, however--it is often helpful to graph the expressions in an inequality before solving algebraically. The practice problems below illustrate the process of solving an inequality algebraically, as well as how to graph the results.

Practice Problem: Find the solution set for the inequality x - 3 > 5

Solution: Manipulate the inequality algebraically, just as you would an equation, to isolate the variable and thereby determine an expression for the solution set.

x - 3 > 5

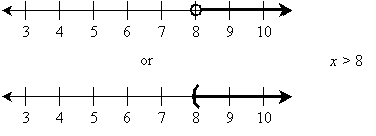
x > 8

The solution set is x > 8, which we can write as the x interval (8, ∞). We can test our answer set by trying several values:

x = 9 : (9) – 3 > 5

6 > 5 (true)

x = 8 : (8) – 3 > 5

5 > 5 (false)

x = 7 : (7) – 3 > 5

4 > 5 (false)

Although testing a few numbers isn't sufficient to verify the correctness of the solution, it is necessary, and we can logically deduce (if we choose the right test numbers) that the solution set is thus correct.

We can plot the solution set on the real number line. Note that we can either use "bracket" notation or open/closed point notation to illustrate whether the endpoint of the interval is included in the solution set.

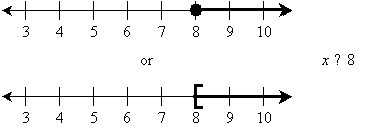
Practice Problem: Find the solution set for the inequality .

For this problem, use the same general approach.

At this point, it becomes apparent that we'll need to do a little more work. Note that for the product of two numbers to be greater than or equal to zero, they must both be greater than or equal to zero, or both less than or equal to zero. So, we can write two separate solutions and simplify the results:

y – 4 ≥ 0 and y + 3 ≥ 0 OR y – 4 ≤ 0 and y + 3 ≤ 0

Simplify each expression:

y ≥ 4 and y ≥ –3 OR y ≤ 4 and y ≤ –3

In each of the two cases, we can reduce the two conditions to one condition, logically:

y ≥ 4 OR y ≤ –3

Our solution set for y is thus the intervals [4, ∞) and (-∞,-3]. The line graph for this solution set is shown below.