|
Diagram
|
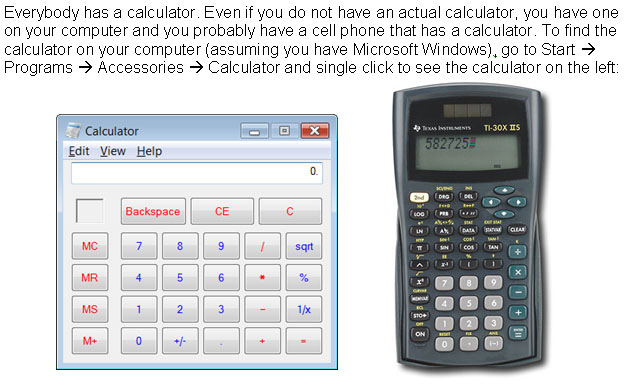
|
Basic Keys and Their Functions
|
Most calculators today are solar powered so simply opening them and putting them where they have light shining on them (the light in your room is enough) will turn them on. However, some also have an "ON" button. If there is an "OFF" button, it is usually the same as the "ON" button.


Most calculators also have a way to clear the last number you put in if you keyed it in wrong:

All calculators have ten number keys in basically the same arrangement:

However, the keys on the cell phone are often arranged with 1, 2, and 3 across the top and 7, 8, and 9 across the third row as seen below.

You will also notice some differences in how addition, subtraction, multiplication, and division keys appear. Once you bring up the calculator function, there is often a circle or square to give you the operations which you perform using the Menu button on the phone. Always put a number in to start and then you can add, subtract, multiply, or divide. A few phones have other operations available, but usually they are available as a download and are quite expensive compared to purchasing a calculator.

The main keys you will need to use on your calculator:


|
Addition, Subtraction, Multiplication and Division
|
To add 18 + 34, key in:
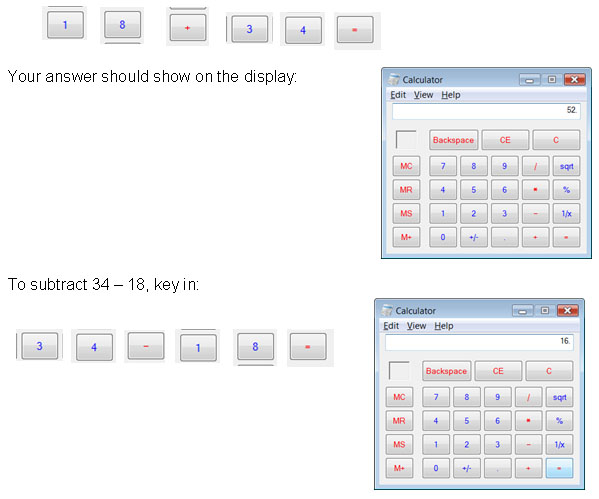

|
Strings of Operations
|
For 3 + 5 – 4 x 2, some calculators will do the indicated operations in order without a problem. However, with some calculators you may need to first do the multiplication, then use the = key, then do the addition and subtraction. Try it each way on your calculator to determine how yours works. If you get 0 for an answer, that is correct.
For multi-step calculations, maintain all significant digits when using a calculator or computer and round off the final value to the appropriate number of significant digits after the calculation.
Problems to try:
6 x 5 + 3 ÷ 2 - 6=
Enter: 6 x 5 + 3 ÷ 2 - 6 = Answer: 25.5
4 ÷ 3(4 x 1015) =
Enter: 4 ÷ 3 x ( 4 x 10 XY 15 ) = Answer: 5.33333333315
3[4 + 6(8 + 2)] =
Enter: 3 x ( 4 + 6 x ( 8 + 2 ) ) = Answer: 192
|
Fractions on a Calculator
|

|
Working with percents and decimals
|
To take 5% of 40:
Remember to change 5% into a decimal which would be 0.05, then key in
.05 x 40 =
This is the standard way of working with percents (as decimals) on all calculators (as well as by hand).
If your calculator has a % function, you can key in
40 x 5% as follows
(this calculator has % as a second function activated by a shift key)

Some calculators have a percent key that essentially divides by 100, but it can do other useful things that might save you a few keystrokes. For instance, if you need to add 5% to a number (perhaps to include the sales tax on a purchase), on most calculators you can enter the original number and then press " + 5 % = ". Just make sure you understand what it does before you blindly trust it. What it is doing in this example is multiplying the original number by 0.05 and then adding the result onto the original number.
Remember that when you put a decimal into your calculator, you do not put in the zero the left of the decimal point, but if there are zeros to the right of the decimal point, put each of those in.
For a problem such as 0.45 x 0.035, key in the decimal and then 4, then 5, then x, then decimal, then 0, then 3, then 5, then =. Your answer will be 0.01575. If you are writing this answer on a sheet of paper, you will have to round it appropriately for significant figures. Since the original factors had 2 significant figures, the answer will have two. Therefore, your answer will be 0.016.
|
Scientific Notation, Powers and Exponents
|
If you just did the problem above (0.45 x 0.035) and got 0.01575, you may want to change that to scientific notation. Every calculator is different in how it deals with scientific notation, so you will need to read your calculator's instructions. If you do not have them or cannot understand them, Google the name and model of your calculator with the word "manual" or "instructions" to see other instructions.
For example, on the Casio fx-260 Solar calculator, you would press "MODE" followed by "8" (that is the scientific mode), followed by the number of significant digits you want which in this case is 2. The answer is 1.6 -02 which means 1.6 x 10-2.
For the calculator on Windows (on your computer), first go to "View" and choose "Scientific". Then work your problem to get 0.01575. Then press the F-E key:
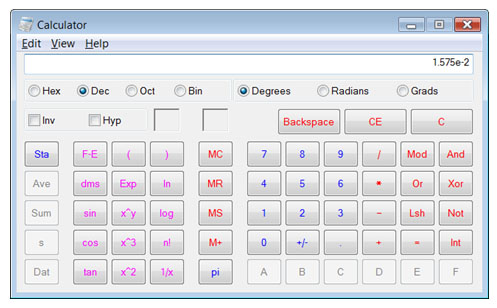
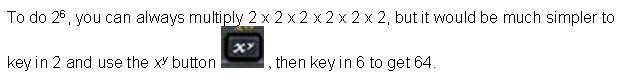
|
Squares and Square Roots
|

Things to keep in mind when using calculator:
- The calculator is a tool to do calculations just as the human mind and paper and pencil are tools. There are many times when mental computing (or even paper & pencil) are more effective or appropriate. For example, adding single digits is done much more quickly using mental math (in your mind) than by punching every number and operation into the calculator. Choosing the right 'tool' is part of effective problem-solving process.
- It is very important to learn how to estimate the result before doing the calculation. It is so very easy to make mistakes when punching in the numbers. Don't 'rely' on the calculator without checking the reasonableness of the answer by estimating.
- On a multiple choice test, calculators should not be used for a random trying out of all possible operations and seeing which one produces the right answer or a given answer.