Key Terms
Objectives
Domain and Range of a Function
We will deal with real-valued functions of real variables--that is, the variables and functions will only have values in the set of real numbers. Furthermore, by just looking at a few examples, we can see that for a given function, sometimes the function or the variable (or both) is limited in the interval of values it can take. In other words, sometimes the function would otherwise not be real-valued for a given real value of the variable, or the function may simply only take on a limited range of values regardless of the value of the independent variable. Consider the case of f(x) = x2. Here, f is defined for any real value x, but f is always greater than or equal to zero--characteristics we can extrapolate by looking at the graph of the function.
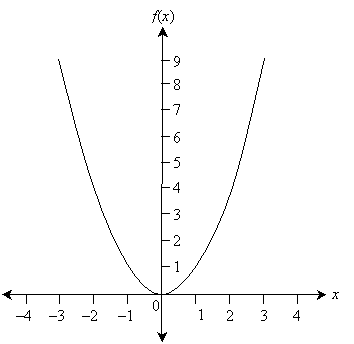
We call the set of values of the independent variable for which the function is defined (typically meaning real-valued) the domain of the function. Concomitantly, we call the set of values of the function itself (corresponding to the entire domain) the range of the function. In the case of f(x) = x2, the domain is the entire set of real numbers (often expressed as 
), since for any real value x, the function f is also real-valued. We can also express this domain as the interval (–∞,∞). The range of f is (as we can see from the graph above) all real values greater than or equal to 0, which we can also express as the interval [0, ∞). To reiterate, the domain of a function f(x) is the set of all values of x for which the function is also real-valued. The range of f(x) is the set of all values of f corresponding to the domain of f.
Practice Problem: Find the domain and range of each function below.
a. 
b. 
c. 
Solution: To find the domain, determine which values for the independent variable will yield a real value for the function. For the range, one option is to graph the function over a representative portion of the domain--alternatively, you can determine the range by inspection.
a. The domain is the interval (–∞, 1), since the denominator must be non-zero and the expression under the radical must be greater than or equal to zero. The graph of the function is shown below to illustrate the range.
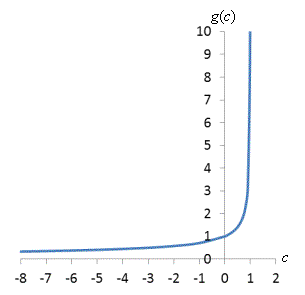
Note that the function approaches (but never reaches) zero as c approaches –∞, and it approaches ∞ as c approaches 1. Thus, the range is (0, ∞).
b. Following an approach similar to that of part a, the domain of h(r) is (–∞, ∞) (or 
) and the range is also (–∞, ∞) (or 
).
c. Because y must be non-negative (greater than or equal to zero), the domain is [0, ∞). The range is also [0, ∞).
Compositions of Functions
A useful tool is a composition of functions (or composite function), which we can describe in one sense as a "function of a function." Consider two functions f(x) and g(x). We define the composite function 
as follows:
For instance, consider f(x) = 3x and g(x) = -x + 4. The composite function
is then
Practice Problem: Given the functions 
and 
, find the following composite functions.
a. 
b. 
Solution: Follow the pattern described above. Plug the expression for one function into the variable for the other according to the required order.
a. 
b.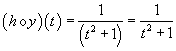 
One-to-One Functions
A function can be described as a mapping of values in the domain to values in the range, as the diagram below illustrates for a function f.
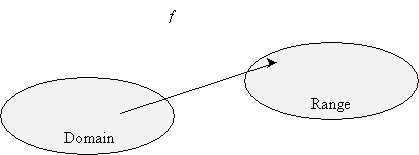
Each value in the domain would be "connected" by an arrow (representing the function) to exactly one value in the range. (Recall that this is a necessary condition for an algebraic relation to be a function: for each value of the independent variable-i.e., the domain-the dependent variable can have only one corresponding value.) But the reverse is not always true: for some functions, certain values in the range may correspond to more than one value in the domain. When each value in the domain corresponds to only one value in the range and each value in the range corresponds to only one value in the domain, the function is called one-to-one. The diagrams below illustrate these differences.
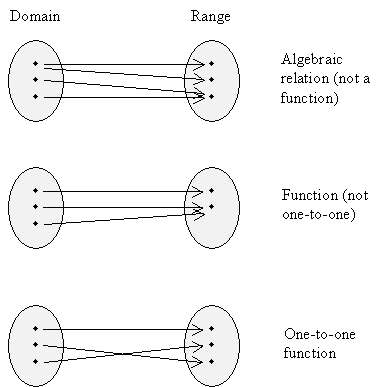
Determining if a function is one-to-one simply by looking at the algebraic expression may be difficult. A simpler way to determine if it is one-to-one is the horizontal line test. Draw a graph of the function and then check if any horizontal line intersects the function more than once. If every horizontal line intersects the function a maximum of one time, then that function is one-to-one. (Note that you can use the nearly identical vertical line test to determine if an algebraic relation is a function: if each vertical line intersects the relation no more than one time, then that relation is a function.)
Inverse of a Function
A function "maps" values in the domain to values in the range by taking a value from the domain as input and outputting the value in the range. But what about a mapping in the opposite direction (from the range to the domain)? This "reverse" mapping is called the inverse of a function. For a function f(x), the inverse is often written as f -1(x). For a function to have an inverse, it must be one-to-one (otherwise, the inverse would not meet the criterion of a function).
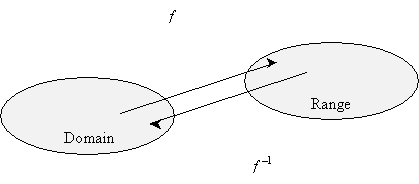
To calculate the inverse, first ensure that the function is one-to-one. Next, perform the following procedure on the original function (which, for simplicity, we'll call f(x)):
1. Substitute f -1(x) for all instances of x.
2. Substitute x for f(x).
3. Solve for f -1(x).
Consider, for instance, f(x) = 5x + 2. This function is one-to-one, and we can find the inverse as follows.
Specifically, for each value x, note the relationship shown in the diagram below.
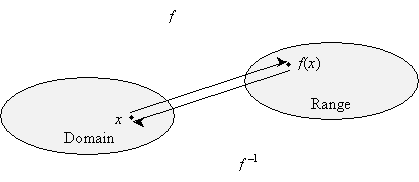
Algebraically, this relationship means that if we plug f(x) into f -1(x), we should get x as the result! (Alternatively, if we plug f -1(x) into f(x), we should also get x.) That is,
Let's try it for the example above:
You can also show that the other composite function yields a result of x as well.
Practice Problem: Determine if the function 
is one-to-one, and if so, calculate its inverse.
Solution: First, we must determine if k(z) is one-to-one. Since this is not easily done just by inspection, let's plot a graph of the function.
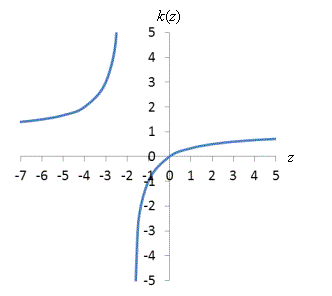
As it turns out, the function passes the horizontal line test (and the vertical line test), so it is one-to-one. Let's calculate the inverse:
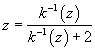
Check the result:
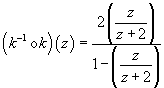
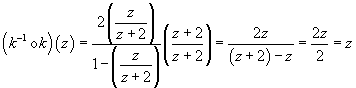
The inverse checks out.
