Objectives

 

Other Conics: Ellipses and Hyperbolas

 

Another conic, the ellipse, is like a somewhat "flattened" circle. The algebraic expression for an ellipse is likewise similar to that for a circle, except that two factors--a and b--are used.

 

 

Note that we can also express a circle as

 

 

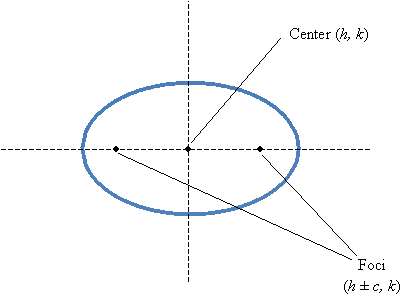
So an ellipse for which a = b = r is a circle of radius r. Like circles, ellipses have a center at (h, k), but they also have two foci (the plural of focus). Instead of a radius, an ellipse has a major axis and a minor axis, with the former having a greater length than the latter.

 

 

 

The major and minor axes are illustrated below for this particular example ellipse.

 

 

 

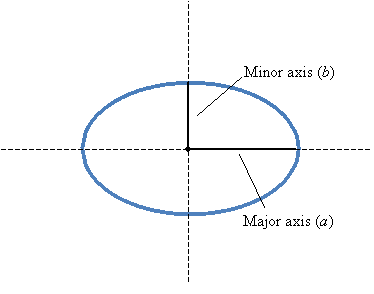
The foci are located at (h ± c, k), where

 

Obviously, these expressions apply when a > b. If b > a, however, then the foci are located at (h, k ± c), where

 

 

 

 

 

 

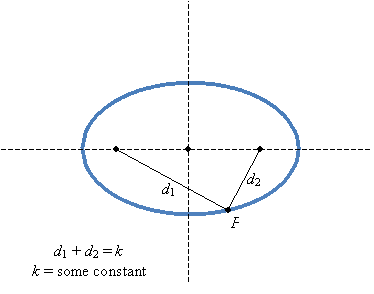
The foci of an ellipse are positioned such that for any point P on the ellipse, the sum of the distances from P to the foci is a constant. Ellipses describe the orbits of celestial bodies (like the planets around the sun) much better than circles. For instance, the Earth follows an elliptical path around the sun, with the sun residing at one of the foci of the ellipse.

 

Practice Problem: For the ellipse below, calculate k. Note that points U and V are the foci.

 

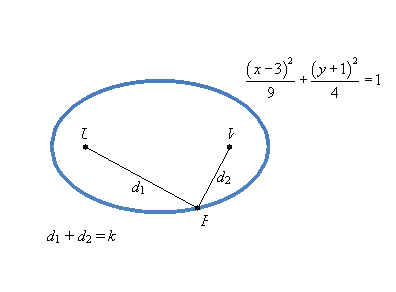
Solution: First, note that d₁ + d₂ = k regardless of the position of P on the ellipse. So, let's simplify the problem. (You can do so in a number of ways-this is one possibility.)

 

 

 

 

 

 

 

 

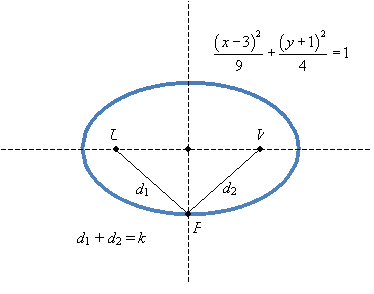
Now, d₁ = d₂ because of the symmetry of the ellipse. From the equation defining ellipse, we know that the distance from the center to the point P is equal to 2; compare the equation with the general form of an ellipse:

 

 

Here, b = 2 is the minor axis. We now only need to calculate the distance from the center to either focus. This distance is c, where

 

 

 

 

 

 

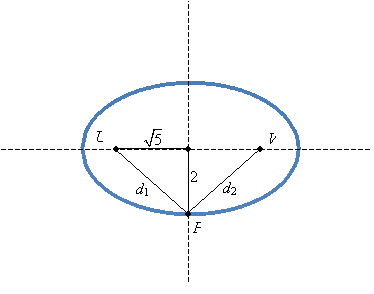
Using the Pythagorean theorem, we can calculate d₁.

 

 

 

 

Then, since d₁ = d₂, k = 6.

 

 

The following is an example of a hyperbola.

 

 

 

 

 

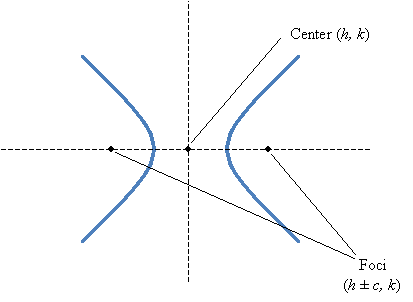
Like an ellipse, a hyperbola has a center (h, k) and foci (h ± c, k). But in this case,

We can also identify the vertices (plural of vertex) of the hyperbola as (h ± a, k). Note that these same points also correspond to what we might call the vertices of the ellipse.

 

 

 

 

 

 

 

 

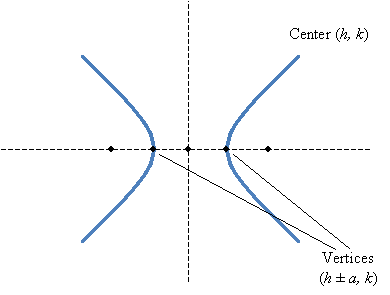
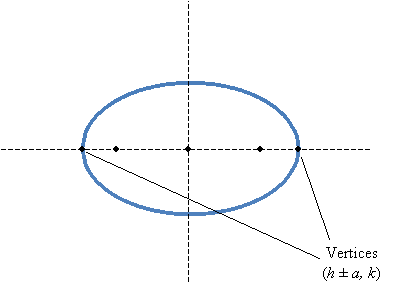
The obvious difference here is that for a hyperbola, the vertices are "inside" the foci; for an ellipse, the vertices are "outside" the foci. Furthermore, hyperbolas (similar to ellipses) obey a fundamental rule regarding the distances between the foci and any point P on the hyperbola. In this case, however, it's the difference rather than the sum of these distances--particularly, the absolute value of the difference.

 

 

 

 

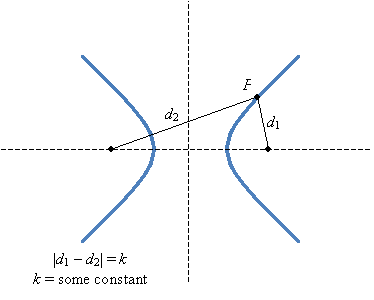
Hyperbolas can also be oriented vertically rather than horizontally. The vertical algebraic representation is

 

Here, the foci are located at (h, k ± c) and the vertices at (h, k ± b). The center is still at (h, k).

 

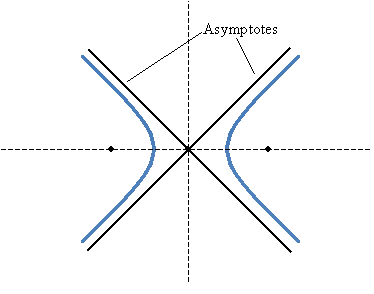
Another characteristic of hyperbolas is that they have two asymptotes that intersect at the center (h, k). Although we will not derive the expressions for these asymptotes, note that they can be written in terms of a, b, h, and k. The asymptotes in the case of a horizontally oriented hyperbola are shown below. Recall that asymptotes are lines that the algebraic relation approaches but never crosses.

 

 

 

 

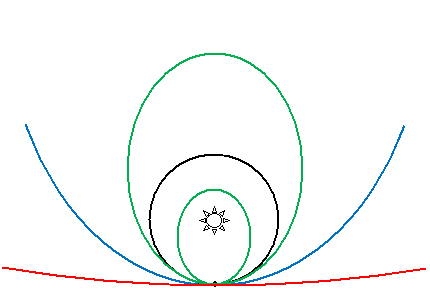
An interesting relationship among all these conics can be seen in the orbits of celestial objects around the sun. In the diagram below, the sun is at the focus of each orbit (in the case of the circular orbit, the "focus" is the center). The point V is the vertex of each orbit (again, in the case of the circle, this is simply some point on the circle). The orbit that an object, like a comet or planet, will take depends on factors like its speed, its mass, and the distance of point V from the sun (the focus). Note that there is only one parabolic orbit (blue) for an object of a given mass and speed. "Outside" of this orbit, all trajectories are hyperbolic (red); "inside," they are elliptical (green), with the special case of the lone circular orbit (black). For a given mass, objects of higher speed at point V will tend toward hyperbolic orbits, whereas those with lower speed will tend toward elliptical orbits. Objects that follow parabolic or elliptical orbits go "around" the sun once, never to return (barring other cosmic factors). Those "inside" the parabola will revolve around the sun indefinitely (again, barring other cosmic factors).