Higher-Degree Polynomials

 

 

Equations involving linear or even quadratic polynomials are fairly straightforward, but if polynomials of higher degrees are involved, the process can be difficult or impossible to do by hand. In these cases, a graphing calculator or computer may be necessary. Nevertheless, we can find the roots of higher-degree polynomials approximately by graphing the functions (even by hand), and in some cases, we can employ a technique called synthetic division to find them and to factor the polynomial.

 

 

A polynomial with a root at x = a has a binomial (x – a) as a factor. Thus, if f(x) is a polynomial of degree n where f(a) = 0, then

 

 

 

 

where g(x) is a polynomial of degree n – 1. Consider a simple example: f(x) = x² – 1. This quadratic polynomial has a root at x = 1, so it has a factor (x – 1):

 

 

 

 

Here, our remaining polynomial g(x) is simply x + 1, which corresponds to the root at x = –1. For a general polynomial f(x) defined as follows,

 

 

 

 

where c_n = 1, the polynomial can be factored into n binomials:

 

 

 

Here, the constants a_i are the roots of f. In other words, a polynomial of degree n has n roots--but these roots may not all be unique, as is the case with x³, which can be factored into the expression (x – 0) (x – 0) (x – 0). (Furthermore, these roots may be complex, as is the case with the quadratic function x² + 1--we will not address this situation, however.) Although this expression factors into three binomials, the corresponding roots are all equal to zero.

 

 

Once you find a root of a polynomial function, you can factor out the corresponding binomial from the polynomial, leaving a lower-degree polynomial as the other factor. Sometimes, this makes finding the remaining roots simple--although sometimes the problem remains just as difficult. To find this lower-degree polynomial, we can use a technique called synthetic division, which is more or less long division of polynomials. Let's consider an example:

 

 

 

 

Say we graphed the function or otherwise determined that one of the roots is at x = 2. We thus know that a factor of f is the binomial x – 2:

 

 

 

 

Here's the procedure for finding g(x).

 

 

1. Set up the division. Draw an inverted division bracket as shown below. Outside the bracket, write the coordinate of the root; inside, write the coefficients of the polynomial that you are factoring from higher-order terms to lower-order terms (include zero-valued coefficients).

 

 

 

 

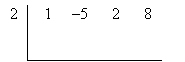
2. Carry the first coefficient. Carry the highest-order coefficient below the bracket.

 

 

 

 

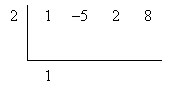
3. Multiply the value of the root by the last value you wrote below the bracket, then write the product under the next coefficient inside the bracket. Now add the values in this column and write the value under the bracket in the same column.

 

 

 

 

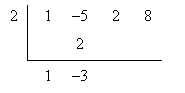
4. Repeat step 3 until you reach the end of the bracket. The final number that you write under the bracket should be zero; if not, either you have made a mistake, or the root value outside the bracket is not a root of the polynomial.

 

 

 

 

 

 

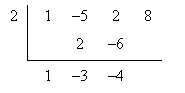
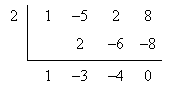
5. Write the new factored polynomial. Use the zero value outside the bracket to write the binomial factor; use the numbers under the bracket as the coefficients for the new polynomial.

 

 

 

 

 

Practice Problem:

The polynomial has a root at x = -2. Find the other roots of the polynomial.

 

 

Solution: First, we can factor out x² from the polynomial to simplify it somewhat.

 

 

 

 

Because the polynomial has a root at x = –2, we know it has a factor (x + 2). Let's use synthetic division to divide out this binomial. First, set up the problem.

 

 

 

 

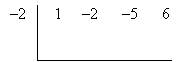
Now, perform the division. Only the result is shown below.

 

 

 

 

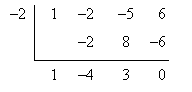
Thus, the polynomial can be expressed as follows:

 

 

 

 

Factor the quadratic:

 

 

 

 

The roots of the polynomial are thus 0 (which occurs "twice"), 1, –2, and 3.

 

 

 

Asymptotes of Rational Functions

 

 

One feature of rational functions that is worth noting is the presence (or absence) of asymptotes: lines that the function gets arbitrarily close to but never touches or crosses. Consider the simple rational function ; a plot of this function is shown below.

 

 

 

 

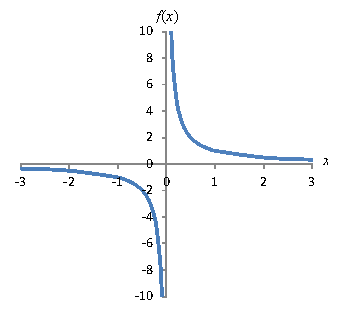
Note that is defined for all x except zero--and this manifests itself as the function getting arbitrarily close to the y-axis but never touching it. In other words, pick your value of x; no matter how small it is, f(x) is defined as long as x isn't zero. Thus, the y-axis (x = 0) is a vertical asymptote of the function . Furthermore, note that no value of x, no matter how large, can make the function equal to zero. Nevertheless, the larger x is, the closer f(x) gets to the x-axis. Thus, the x-axis (y = 0) is a horizontal asymptote of . These asymptotes are added to the graph below.

 

 

 

 

Asymptotes can be any line on the coordinate plane, and finding the expressions for those lines can sometimes be difficult. Simple cases, like above, also crop up. Note that whenever the domain (or range) has the form (a, b) and (b, c), an asymptote exists for the independent (or dependent) variable value b. Note that for , for example, the domain is (-∞, 0) and (0, ∞). Thus, an asymptote exists at x = 0. (Note also that not all asymptotes correspond to functions! Any asymptote x = a is a line, but it is not a function.)

 

 

An additional point to note about asymptotes is that the function may actually cross an asymptote at some point, but this crossing is not related to the part of the function that exhibits asymptotic behavior. That is, the function might approach the asymptote as the independent variable gets very large, but it might also cross the asymptote at a small value of x, like x = 0. This crossing does not mean the asymptote doesn't exist.

 

 

 

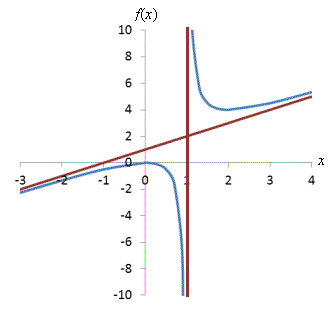
Practice Problem: Graph the function and find its asymptotes. You need not determine the functions for those asymptotes.

 

 

Solution: First, graph the function.

 

 

 

 

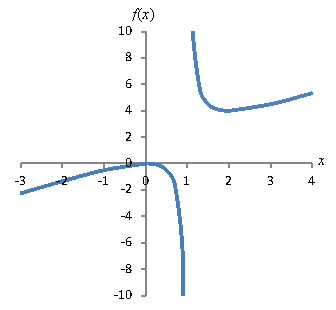
Clearly, the function has an asymptote at x = 1: this corresponds to the root of the polynomial in the denominator of the function. Slightly less obvious, however, is the presence of another, "diagonal" asymptote. As it turns out, this asymptote corresponds to the line x + 1 (how precisely this is calculated is beyond the scope of this article). A non-vertical, non-horizontal asymptote is called a slant asymptote.